
【題目】如圖,點O在邊長為6![]() 的正方形ABCD的對角線AC上,以O為圓心OA為半徑的⊙O交AB于點E.
的正方形ABCD的對角線AC上,以O為圓心OA為半徑的⊙O交AB于點E.
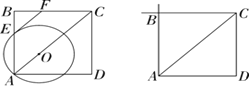
(1)⊙O過點E的切線與BC交于點F,當0<OA<6時,求∠BFE的度數;
(2)設⊙O與AB的延長線交于點M,⊙O過點M的切線交BC的延長線于點N,當6<OA<12時,利用備用圖作出圖形,求∠BNM的度數.
【答案】(1)∠BFE=45°;(2)∠BNM=45°.
【解析】
(1)連結OE,根據圓的半徑都相等可得OA=OE,再根據等邊對等角可得∠EAO=∠AEO,接下來再根據正方形以及切線性質即可得到∠BEF=45°,至此,再根據三角形內角和是180°即可得到∠BFE的度數了;
(2)根據題意畫出圖形,連結OM,根據等邊對等角的性質和正方形的性質可得∠OAM=∠AMO=45°,至此,再根據切線的性質以及三角形內角和定理進行求解即可;
(1)連接OE,如解圖,
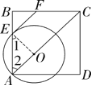
∵四邊形ABCD為正方形,∴∠2=45°,
∵OE=OA,∴∠1=∠2=45°,
∵EF為⊙O的切線,∴OE⊥EF,
∴∠OEF=90°,∴∠BEF=45°,
∵∠B=90°,
∴∠BFE=45°;
(2)連接OM,如解圖,
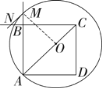
∵OM=OA,
∴∠OMA=∠OAM=45°,
∵MN為⊙O的切線,∴OM⊥MN,
∴∠OMN=90°,∴∠BMN=45°,
∵∠MBN=90°,∴∠BNM=45°.


 每課必練系列答案
每課必練系列答案 巧學巧練系列答案
巧學巧練系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數y=﹣x2+2x+m.
(1)如果二次函數的圖象與x軸有兩個交點,求m的取值范圍;
(2)如圖,二次函數的圖象過點A(3,0),與y軸交于點B,直線AB與這個二次函數圖象的對稱軸交于點P,求點P的坐標.
(3)根據圖象直接寫出使一次函數值大于二次函數值的x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
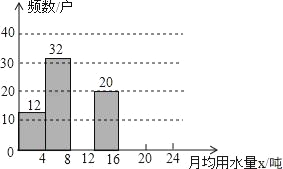
【題目】2014年,河北省委宣傳部主辦“河北節約之星”活動,表彰節水先進典型,省委宣傳部號召全社會以節水先進典型為榜樣,牢固樹立節約用水理念,爭做節儉美德的傳承者,節約用水的踐行者.小鵬想了解某小區住戶月均用水情況,隨機調查了該小區部分住戶,并將調查數據繪制成如圖所示的頻數分布直方圖(不完整)和如下的頻數分布表.
月均用水量x(噸) | 頻數(戶) | 頻率 |
0<x≤4 | 12 | a |
4<x≤8 | 32 | 0.32 |
8<x≤12 | b | c |
12<x≤16 | 20 | 0.2 |
16<x≤20 | 8 | 0.08 |
20<x≤24 | 4 | 0.04 |
(1)求a,b,c的值,并將如圖所示的頻數分布直方圖補充完整;
(2)求月均用水量超過12噸的住戶占所調查總住戶的百分比;
(3)若該小區有1000住戶,根據所調查的數據,該小區月均用水量沒有超過8噸的住戶有多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
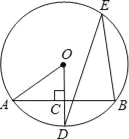
【題目】如圖所示,AB是⊙O的一條弦,OD⊥AB,垂足為C,交⊙O于點D,點E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度數;
(2)若OC=3,OA=5,求AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,梯形ABCD中,AB∥CD,AB=14,AD= 4![]() , CD=7.直線l經過A,D兩點,且sin∠DAB=
, CD=7.直線l經過A,D兩點,且sin∠DAB=![]() . 動點P在線段AB上從點A出發以每秒2個單位的速度向點B運動,同時動點Q從點B出發以每秒5個單位的速度沿B→C→D的方向向點D運動,過點P作PM垂直于AB,與折線A→D→C相交于點M,當P,Q兩點中有一點到達終點時,另一點也隨之停止運動.設點P,Q運動的時間為t秒(t>0),△MPQ的面積為S.
. 動點P在線段AB上從點A出發以每秒2個單位的速度向點B運動,同時動點Q從點B出發以每秒5個單位的速度沿B→C→D的方向向點D運動,過點P作PM垂直于AB,與折線A→D→C相交于點M,當P,Q兩點中有一點到達終點時,另一點也隨之停止運動.設點P,Q運動的時間為t秒(t>0),△MPQ的面積為S.
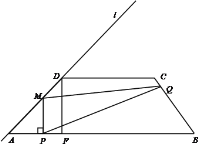
(1)求腰BC的長;
(2)當Q在BC上運動時,求S與t的函數關系式;
(3)在(2)的條件下,是否存在某一時刻t,使得△MPQ的面積S是梯形ABCD面積的![]() ?若存在,請求出t的值;若不存在,請說明理由;
?若存在,請求出t的值;若不存在,請說明理由;
(4)隨著P,Q兩點的運動,當點M在線段DC上運動時,設PM的延長線與直線l相交于點N,試探究:當t為何值時,△QMN為等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
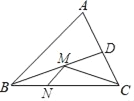
【題目】如圖,在銳角三角形ABC中,BC=6![]() ,∠ABC=45°,BD平分∠ABC,M、N分別是BD、BC上的動點,則CM+MN的最小值是_____.
,∠ABC=45°,BD平分∠ABC,M、N分別是BD、BC上的動點,則CM+MN的最小值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
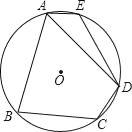
【題目】如圖,在⊙O的內接四邊形ABCD中,AB=AD,∠C=120°,點E在![]() 上.
上.
(1)求∠E的度數;
(2)連接OD、OE,當∠DOE=90°時,AE恰好為⊙O的內接正n邊形的一邊,求n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 是垂直于水平面的一棵樹,小馬(身高1.70米)從點
是垂直于水平面的一棵樹,小馬(身高1.70米)從點![]() 出發,先沿水平方向向左走10米到
出發,先沿水平方向向左走10米到![]() 點,再經過一段坡度
點,再經過一段坡度![]() ,坡長為5米的斜坡
,坡長為5米的斜坡![]() 到達
到達![]() 點,然后再沿水平方向向左行走5米到達
點,然后再沿水平方向向左行走5米到達![]() 點(
點(![]() 、
、![]() 、
、![]() 、
、![]() 在同一平面內),小馬在線段
在同一平面內),小馬在線段![]() 的黃金分割點
的黃金分割點![]() 處(
處(![]() )測得大樹的頂端
)測得大樹的頂端![]() 的仰角為37°,則大樹
的仰角為37°,則大樹![]() 的高度約為( )米.(參考數據:
的高度約為( )米.(參考數據:![]() )
)
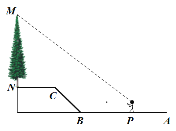
A. 7.8米 B. 8.0米 C. 8.1米 D. 8.3米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com