
題目列表(包括答案和解析)
如圖,某地為了開發旅游資源,欲修建一條連接風景點![]() 和居民區
和居民區![]() 的公路,點
的公路,點![]() 所在的山坡面與山腳所在水平面
所在的山坡面與山腳所在水平面![]() 所成的二面角為
所成的二面角為![]() (
(![]() ),且
),且![]() ,點
,點![]() 到平面
到平面![]() 的距離
的距離![]() (km).沿山腳原有一段筆直的公路
(km).沿山腳原有一段筆直的公路![]() 可供利用.從點
可供利用.從點![]() 到山腳修路的造價為
到山腳修路的造價為![]() 萬元/km,原有公路改建費用為
萬元/km,原有公路改建費用為![]() 萬元/km.當山坡上公路長度為
萬元/km.當山坡上公路長度為![]() km(
km(![]() )時,其造價為
)時,其造價為![]() 萬元.已知
萬元.已知![]() ,
,![]() ,
,![]() ,
,![]() .
.
(I)在![]() 上求一點
上求一點![]() ,使沿折線
,使沿折線![]() 修建公路的總造價最小;
修建公路的總造價最小;
(II) 對于(I)中得到的點![]() ,在
,在![]() 上求一點
上求一點![]() ,使沿折線
,使沿折線![]() 修建公路的總造價最小.
修建公路的總造價最小.
(III)在![]() 上是否存在兩個不同的點
上是否存在兩個不同的點![]() ,
,![]() ,使沿折線
,使沿折線![]() 修建公路的總造價小于(II)中得到的最小總造價,證明你的結論.
修建公路的總造價小于(II)中得到的最小總造價,證明你的結論.

(I)在![]() 上求一點
上求一點![]() ,使沿折線
,使沿折線![]() 修建公路的總造價最小;
修建公路的總造價最小;
(II) 對于(I)中得到的點![]() ,在
,在![]() 上求一點
上求一點![]() ,使沿折線
,使沿折線![]() 修建公路的總造價最小.
修建公路的總造價最小.
(III)在![]() 上是否存在兩個不同的點
上是否存在兩個不同的點![]() 、
、![]() ,使沿折線
,使沿折線![]() 修建公路的總造價小于(II)中得到的最小總造價,證明你的結論.
修建公路的總造價小于(II)中得到的最小總造價,證明你的結論.
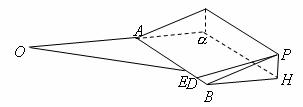
圖4
(本小題滿分13分)
已知,在水平平面 上有一長方體
上有一長方體 繞
繞 旋轉
旋轉 得到如圖所示的幾何體.
得到如圖所示的幾何體.
(Ⅰ)證明:平面 平面
平面 ;
;
(Ⅱ)當 時,直線
時,直線 與平面
與平面 所成的角的正弦值為
所成的角的正弦值為 ,求
,求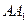 的長度;
的長度;
(Ⅲ)在(Ⅱ)條件下,設旋轉過程中,平面 與平面
與平面 所成的角為
所成的角為 ,
, 長方體
長方體 的最高點離平面
的最高點離平面 的距離為
的距離為 ,請直接寫出
,請直接寫出 的一個表達式,并注明定義域.
的一個表達式,并注明定義域.
(本小題滿分13分)
已知,在水平平面 上有一長方體
上有一長方體 繞
繞 旋轉
旋轉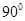 得到如圖所示的幾何體.
得到如圖所示的幾何體.

(Ⅰ)證明:平面 平面
平面 ;
;
(Ⅱ)當 時,直線
時,直線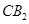 與平面
與平面 所成的角的正弦值為
所成的角的正弦值為 ,求
,求 的長度;
的長度;
(Ⅲ)在(Ⅱ)條件下,設旋轉過程中,平面 與平面
與平面 所成的角為
所成的角為 ,長方體
,長方體 的最高點離平面
的最高點離平面 的距離為
的距離為 ,請直接寫出
,請直接寫出 的一個表達式,并注明定義域.
的一個表達式,并注明定義域.
(本小題滿分13分)
已知,在水平平面 上有一長方體
上有一長方體 繞
繞 旋轉
旋轉 得到如圖所示的幾何體.
得到如圖所示的幾何體.

(Ⅰ)證明:平面 平面
平面 ;
;
(Ⅱ)當 時,直線
時,直線 與平面
與平面 所成的角的正弦值為
所成的角的正弦值為 ,求
,求 的長度;
的長度;
(Ⅲ)在(Ⅱ)條件下,設旋轉過程中,平面 與平面
與平面 所成的角為
所成的角為 ,長方體
,長方體 的最高點離平面
的最高點離平面 的距離為
的距離為 ,請直接寫出
,請直接寫出 的一個表達式,并注明定義域.
的一個表達式,并注明定義域.
一、DDBCD CABCA
二、11.1;
12. ; 13.
; 13. 14.
14. ; 15.
; 15. ;
;
16.
三.解答題(本大題共6小題,共76分)
17.解:(1)法一:由題可得 ;
;
法二:由題 ,
,
故 ,從而
,從而 ;
;
法三:由題 ,解得
,解得 ,
,
故 ,從而
,從而 。
。
(2) ,令
,令 ,
,
則 ,
,
 在
在 單調遞減,
單調遞減,
故
 ,
,
從而 的值域為
的值域為 。
。
18.解:(1) 的可能取值為0,1,2,3,4,
的可能取值為0,1,2,3,4, ,
,

 ,
,
 ,
, ,
,
 。
。
因此隨機變量 的分布列為下表所示;
的分布列為下表所示;

0
1
2
3
4






(2)由⑴得: ,
,

19.法一:(1)連接 ,設
,設 ,則
,則 。
。
因為 ,所以
,所以 ,故
,故 ,從而
,從而 ,
,
故 。
。
又因為 ,
,
所以 ,當且僅當
,當且僅當 取等號。
取等號。
此時 為
為 邊的中點,
邊的中點, 為
為 邊的中點。
邊的中點。
故當 為
為 邊的中點時,
邊的中點時, 的長度最小,其值為
的長度最小,其值為
(2)連接 ,因為此時
,因為此時 分別為
分別為 的中點,
的中點,
故 ,所以
,所以 均為直角三角形,
均為直角三角形,
從而 ,所以
,所以 即為直線
即為直線 與平面
與平面 所成的角。
所成的角。
因為 ,所以
,所以 即為所求;
即為所求;
(3)因 ,又
,又 ,所以
,所以 。
。
又 ,故三棱錐
,故三棱錐 的表面積為
的表面積為
 。
。
因為三棱錐 的體積
的體積 ,
,
所以 。
。
法二:(1)因 ,故
,故 。
。
設 ,則
,則 。
。
所以 ,
,
當且僅當 取等號。此時
取等號。此時 為
為 邊的中點。
邊的中點。
故當 為
為 的中點時,
的中點時, 的長度最小,其值為
的長度最小,其值為 ;
;
(2)因 ,又
,又 ,所以
,所以 。
。
記 點到平面
點到平面 的距離為
的距離為 ,
,
因 ,故
,故 ,解得
,解得 。
。
 因
因 ,故
,故 ;
;
(3)同“法一”。
法三:(1)如圖,以 為原點建立空間直角坐標系,設
為原點建立空間直角坐標系,設 ,則
,則 ,
,
所以 ,當且僅當
,當且僅當 取等號。
取等號。
此時 為
為 邊的中點,
邊的中點, 為
為 邊的中點。
邊的中點。
故當 為
為 邊的中點時,
邊的中點時, 的長度最小,其值為
的長度最小,其值為 ;
;
(2)設 為面
為面 的法向量,因
的法向量,因 ,
,
故 。取
。取 ,得
,得 。
。
又因 ,故
,故 。
。
因此 ,從而
,從而 ,
,
所以 ;
;
(3)由題意可設 為三棱錐
為三棱錐 的內切球球心,
的內切球球心,
則 ,可得
,可得 。
。
與(2)同法可得平面 的一個法向量
的一個法向量 ,
,
又 ,故
,故 ,
,
解得 。顯然
。顯然 ,故
,故 。
。
20.解:(1)當 時,
時, 。令
。令 得
得 ,
,
故當 時
時 ,
, 單調遞增;
單調遞增;
當 時
時 ,
, 單調遞減。
單調遞減。
所以函數 的單調遞增區間為
的單調遞增區間為 ,
,
單調遞減區間為 ;
;
(2)法一:因 ,故
,故 。
。
令 ,
,
要使 對滿足
對滿足 的一切
的一切 成立,則
成立,則 ,
,
解得 ;
;
法二: ,故
,故 。
。
由 可解得
可解得 。
。
因為 在
在 單調遞減,因此
單調遞減,因此 在
在 單調遞增,故
單調遞增,故 。設
。設 ,
,
則 ,因為
,因為 ,
,
所以 ,從而
,從而 在
在 單調遞減,
單調遞減,
故 。因此
。因此 ,即
,即 。
。
(3)因為 ,所以
,所以
即 對一切
對一切 恒成立。
恒成立。
 ,令
,令 ,
,
則 。因為
。因為 ,所以
,所以 ,
,
故 在
在 單調遞增,有
單調遞增,有 。
。
因此 ,從而
,從而 。
。
所以 。
。
21.解:(1)設 ,則由題
,則由題 ,
,
由 得
得 ,故
,故 。
。
又根據 可得
可得 ,
,
即 ,代入可得
,代入可得 ,
,
解得 (舍負)。故
(舍負)。故 的方程為
的方程為 ;
;
(2)法一:設 ,代入
,代入 得
得 ,
,
故 ,
,
從而


因此 。
。
法二:顯然點 是拋物線
是拋物線 的焦點,點
的焦點,點 是其準線
是其準線 上一點。
上一點。
設 為
為 的中點,過
的中點,過 分別作
分別作 的垂線,垂足分別為
的垂線,垂足分別為 ,
,
則 。
。
因此以 為直徑的圓與準線
為直徑的圓與準線 相切(于點
相切(于點 )。
)。
若 與
與 重合,則
重合,則 。否則點
。否則點 在
在 外,因此
外,因此 。
。
綜上知 。
。
22.證明:(1)因 ,故
,故 。
。
顯然 ,因此數列
,因此數列 是以
是以 為首項,以2為公比的等比數列;
為首項,以2為公比的等比數列;
(2)由⑴知 ,解得
,解得 ;
;
(3)因為

所以 。
。
又
 (當且僅當
(當且僅當 時取等號),
時取等號),
故 。
。
綜上可得 。(亦可用數學歸納法)
。(亦可用數學歸納法)
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com