
(I)在![]() 上求一點
上求一點![]() ,使沿折線
,使沿折線![]() 修建公路的總造價最小;
修建公路的總造價最小;
(II) 對于(I)中得到的點![]() ,在
,在![]() 上求一點
上求一點![]() ,使沿折線
,使沿折線![]() 修建公路的總造價最小.
修建公路的總造價最小.
(III)在![]() 上是否存在兩個不同的點
上是否存在兩個不同的點![]() 、
、![]() ,使沿折線
,使沿折線![]() 修建公路的總造價小于(II)中得到的最小總造價,證明你的結論.
修建公路的總造價小于(II)中得到的最小總造價,證明你的結論.
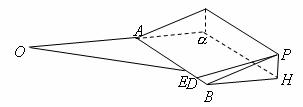
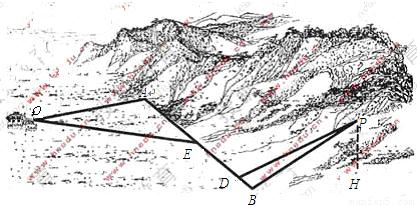
圖4
解:(I)如圖,![]() ,
,![]() ,
,![]() ,由三垂線定理逆定理知,
,由三垂線定理逆定理知,![]() ,所以
,所以![]() 是山坡與
是山坡與![]() 所成二面角的平面角,則
所成二面角的平面角,則![]() ,
,

![]() .
.
設![]() ,
,![]() .則
.則![]()
![]() .
.
記總造價為![]() 萬元,
萬元,
據題設有![]()
![]()
當![]() ,即
,即![]() 時,總造價
時,總造價![]() 最小.
最小.
(II)設![]() ,
,![]() ,總造價為
,總造價為![]() 萬元,根據題設有
萬元,根據題設有
![]()
![]() .
.
則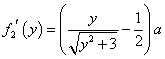 ,由
,由![]() ,得
,得![]() .
.
當![]() 時,
時,![]() ,
,![]() 在
在![]() 內是減函數;
內是減函數;
當![]() 時,
時,![]() ,
,![]() 在
在![]() 內是增函數.
內是增函數.
故當![]() ,即
,即![]() (km)時總造價
(km)時總造價![]() 最小,且最小總造價為
最小,且最小總造價為![]() 萬元.
萬元.
(III)解法一:不存在這樣的點![]() ,
,![]() .
.
事實上,在![]() 上任取不同的兩點
上任取不同的兩點![]() ,
,![]() .為使總造價最小,
.為使總造價最小,![]() 顯然不能位于
顯然不能位于![]() 與
與![]() 之間.故可設
之間.故可設![]() 位于
位于![]() 與
與![]() 之間,且
之間,且![]() =
=![]() ,
,![]() ,
,![]() ,總造價為
,總造價為![]() 萬元,則
萬元,則![]() .類似于(I)、(II)的討論知,
.類似于(I)、(II)的討論知,![]() ,
,![]() ,當且僅當
,當且僅當![]() ,
,![]() 同時成立時,上述兩個不等式等號同時成立,此時
同時成立時,上述兩個不等式等號同時成立,此時![]() ,
,![]() ,
,![]() 取得最小值
取得最小值![]() ,點
,點![]() 分別與點
分別與點![]() 重合,所以不存在這樣的點
重合,所以不存在這樣的點![]() ,使沿折線
,使沿折線![]() 修建公路的總造價小于(II)中得到的最小總造價.
修建公路的總造價小于(II)中得到的最小總造價.
解法二:同解法一得
![]()
![]()
![]()
![]() .
.
當且僅當![]() 且
且![]() ,即
,即![]() 同時成立時,
同時成立時,![]() 取得最小值
取得最小值![]() ,以下同解法一.
,以下同解法一.


 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:高中數學 來源: 題型:
| 2 |
| 5 |
| a |
| 2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(07年湖南卷理)(12分)
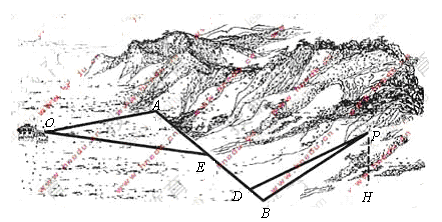
如圖4,某地為了開發旅游資源,欲修建一條連接風景點![]() 和居民區
和居民區![]() 的公路,點
的公路,點![]() 所在的山坡面與山腳所在水平面
所在的山坡面與山腳所在水平面![]() 所成的二面角為
所成的二面角為![]() (
(![]() ),且
),且![]() ,點
,點![]() 到平面
到平面![]() 的距離
的距離![]() (km).沿山腳原有一段筆直的公路
(km).沿山腳原有一段筆直的公路![]() 可供利用.從點
可供利用.從點![]() 到山腳修路的造價為
到山腳修路的造價為![]() 萬元/km,原有公路改建費用為
萬元/km,原有公路改建費用為![]() 萬元/km.當山坡上公路長度為
萬元/km.當山坡上公路長度為![]() km(
km(![]() )時,其造價為
)時,其造價為![]() 萬元.已知
萬元.已知![]() ,
,![]() ,
,![]() ,
,![]() .
.
(I)在![]() 上求一點
上求一點![]() ,使沿折線
,使沿折線![]() 修建公路的總造價最小;
修建公路的總造價最小;
(II) 對于(I)中得到的點![]() ,在
,在![]() 上求一點
上求一點![]() ,使沿折線
,使沿折線![]()
修建公路的總造價最小.
(III)在![]() 上是否存在兩個不同的點
上是否存在兩個不同的點![]() ,
,![]() ,使沿折線
,使沿折線![]() 修建公路的
修建公路的
總造價小于(II)中得到的最小總造價,證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
(1)在AB上求一點D,使沿折線PDAO修建公路的總造價最小;
(2)對于(1)中得到的點D,在DA上求一點E,使沿折線PDEO修建公路的總造價最小;
(3)在AB上是否存在兩個不同的點D′,E′,使沿折線.PD′E′O修建公路的總造價小于(2)中得到的最小總造價?證明你的結論.

a)
第19題圖
(文)如圖b所示,直四棱柱ABCD-A1B1C1D1中,∠ADC=90°,△ABC為等邊三角形,且AA1=AD=DC=2.
(1)求AC1與BC所成角的余弦值;
(2)求二面角C1-BD-C的大小;
(3)設M是BD上的點,當DM為何值時,D1M⊥平面A1C1D?并證明你的結論.

第19題圖
查看答案和解析>>
科目:高中數學 來源:2007年湖南省高考數學試卷(理科)(解析版) 題型:解答題
 ,點P到平面α的距離PH=0.4(km).沿山腳原有一段筆直的公路AB可供利用、從點O到山腳修路的造價為a萬元/km,原有公路改建費用為
,點P到平面α的距離PH=0.4(km).沿山腳原有一段筆直的公路AB可供利用、從點O到山腳修路的造價為a萬元/km,原有公路改建費用為 萬元/km、當山坡上公路長度為lkm(1≤l≤2)時,其造價為(l2+1)a萬元、已知OA⊥AB,PB⊥AB,AB=1.5(km),
萬元/km、當山坡上公路長度為lkm(1≤l≤2)時,其造價為(l2+1)a萬元、已知OA⊥AB,PB⊥AB,AB=1.5(km), .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com