
題目列表(包括答案和解析)
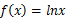 ,
,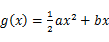 (
(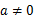 )
)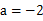 時(shí),函數(shù)
時(shí),函數(shù)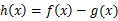 在其定義域是增函數(shù),求b的取值范圍。
在其定義域是增函數(shù),求b的取值范圍。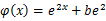 ,
,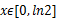 ,求函數(shù)
,求函數(shù)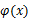 的最小值
的最小值
函數(shù)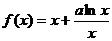 ,其中
,其中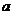 為常數(shù).
為常數(shù).
(1)證明:對任意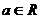 ,
,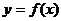 的圖象恒過定點(diǎn);
的圖象恒過定點(diǎn);
(2)當(dāng)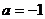 時(shí),判斷函數(shù)
時(shí),判斷函數(shù)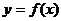 是否存在極值?若存在,求出極值;若不存在,說明理由;
是否存在極值?若存在,求出極值;若不存在,說明理由;
(3)若對任意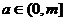 時(shí),
時(shí),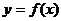 恒為定義域上的增函數(shù),求
恒為定義域上的增函數(shù),求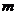 的最大值.
的最大值.
函數(shù)![]() ,其中a為常數(shù).
,其中a為常數(shù).
(1)證明:對任意a∈R,y=f(x)的圖象恒過定點(diǎn);
(2)當(dāng)a=-1時(shí),判斷函數(shù)y=f(x)是否存在極值?若存在,求出極值;若不存在,說明理由;
(3)若對任意a∈(0,m]時(shí),y=f(x)恒為定義域上的增函數(shù),求m的最大值.
已知![]()
(1)若![]() ,函數(shù)
,函數(shù)![]() 在其定義域內(nèi)是增函數(shù),求
在其定義域內(nèi)是增函數(shù),求![]() 的取值范圍;
的取值范圍;
(2)當(dāng)![]() 時(shí),證明:函數(shù)
時(shí),證明:函數(shù)![]() 只有一個(gè)零點(diǎn);
只有一個(gè)零點(diǎn);
(3)若![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 兩
兩![]() 點(diǎn),AB
點(diǎn),AB![]() 中點(diǎn)為
中點(diǎn)為![]() ,求證:
,求證:![]()
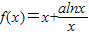 ,其中a為常數(shù).
,其中a為常數(shù).一、選擇題

二、填空題
13. ; 14.112; 15.
; 14.112; 15. ; 16.
; 16.
三、解答題
17.解:∵向量 的夾角
的夾角 ,
,

①當(dāng) 時(shí),
時(shí), ;②當(dāng)
;②當(dāng) 時(shí),
時(shí), ;③當(dāng)
;③當(dāng) 時(shí),
時(shí),

綜上所述:當(dāng) 時(shí),
時(shí),  的范圍是
的范圍是 當(dāng)
當(dāng) 時(shí),
時(shí), 的范圍是
的范圍是 ;
;
當(dāng) 時(shí),
時(shí),  的范圍是
的范圍是
18.解:(1) ∵ 底面ABC,∴
底面ABC,∴ .又∵
.又∵ 是正三角形,且E為AC的中點(diǎn),
是正三角形,且E為AC的中點(diǎn), .又
.又 ,
, 平面PAC.
平面PAC. 平面PEF,
平面PEF,
∴平面 平面PAC.
平面PAC.
(2)取CD的中點(diǎn)F,則點(diǎn)F即為所求.∵E、F分別為CA、CD的中點(diǎn), .
.
又 平面PEF,
平面PEF, 平面PEF,∴
平面PEF,∴ 平面PEF.
平面PEF.
(3) .
.
19.解:(1)

依題意
 ,
,




(2)
又
在Rt△ABC中,

又
20.解:(I) ,
,
由 ,
,  ,
,
 ,
,
 ,
, ,∴
,∴ 。
。
(II)由 得:
得:
 ,
,
 ,
, ,
,
由②-①得:

 。
。
21解:當(dāng)年生產(chǎn)x(萬件)時(shí),
年生產(chǎn)成本=固定費(fèi)用+年生產(chǎn)費(fèi)用 ,
,
年銷售收入 ,∵利潤=銷售收入―生產(chǎn)成本―促銷費(fèi),
,∵利潤=銷售收入―生產(chǎn)成本―促銷費(fèi),
∴

 (萬元).
(萬元).
當(dāng)切僅當(dāng) 即
即 時(shí),
時(shí),
∴該企業(yè)2008年的促銷費(fèi)投入7萬元時(shí),企業(yè)的年利潤 (萬元)最大.
(萬元)最大.
22.解:(1)依題意: ∵
∵ 上是增函數(shù),
上是增函數(shù),
∴ 恒成立,
恒成立,
∴ ∵
∵ ∴b的取值范圍為
∴b的取值范圍為
(2)設(shè) 則函數(shù)化為
則函數(shù)化為 ,
,
∵ ∴當(dāng)
∴當(dāng) 上為增函數(shù),
上為增函數(shù),
當(dāng) 時(shí),
時(shí), 當(dāng)
當(dāng)
 當(dāng)
當(dāng) 上為減函數(shù),
上為減函數(shù),
當(dāng) 時(shí),
時(shí), 綜上所述,當(dāng)
綜上所述,當(dāng)
當(dāng) 時(shí),
時(shí), ;
;
(3)設(shè)點(diǎn)P、Q的坐標(biāo)是
則點(diǎn)M、N的橫坐標(biāo)為 C1在M處的切線斜率為
C1在M處的切線斜率為
C2在點(diǎn)N處的切線斜率
假設(shè)C1在點(diǎn)M處的切線與C2在點(diǎn)N處的切線平行,則
即 則
則




 。設(shè)
。設(shè) 。
。
令 則
則
∵ ∴
∴ 所以
所以 上單調(diào)遞增,故
上單調(diào)遞增,故 ,則
,則 這與①矛盾,假設(shè)不成立,故C1在點(diǎn)M處的切線與C2在點(diǎn)N處的切線不平行。
這與①矛盾,假設(shè)不成立,故C1在點(diǎn)M處的切線與C2在點(diǎn)N處的切線不平行。
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com