
題目列表(包括答案和解析)
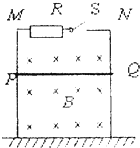 平行金屬導軌MN豎直放置于絕緣水平地板上,如右圖所示,金屬桿PQ可以緊貼導軌無摩擦滑動,導軌間除固定電阻R以外,其它部分電阻不計,勻強磁場B垂直穿過導軌平面,以下有兩種情況:第1次,先閉合開關S,然后從圖中位置由靜止釋放PQ,經一段時間后PQ勻速到達地面;第2次,先從同一高度由靜止釋放PQ,當PQ下滑一段距離后突然閉合開關S,最終PQ也勻速到達了地面.設上述兩種情況PQ由于切割磁感線產生的電能分別為W1、W2,則可以判定( )
平行金屬導軌MN豎直放置于絕緣水平地板上,如右圖所示,金屬桿PQ可以緊貼導軌無摩擦滑動,導軌間除固定電阻R以外,其它部分電阻不計,勻強磁場B垂直穿過導軌平面,以下有兩種情況:第1次,先閉合開關S,然后從圖中位置由靜止釋放PQ,經一段時間后PQ勻速到達地面;第2次,先從同一高度由靜止釋放PQ,當PQ下滑一段距離后突然閉合開關S,最終PQ也勻速到達了地面.設上述兩種情況PQ由于切割磁感線產生的電能分別為W1、W2,則可以判定( )| A、W1>W2 | B、W1=W2 | C、W1<W2 | D、以上結論都不正確 |
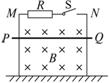
圖1-8
A.W1>W2 B.W1=W2
C.W1<W2 ? D.以上結論都不正確
 如圖所示,“×”型光滑金屬導軌abcd固定在絕緣水平面上,ab和cd足夠長,∠aOc=60°.虛線MN與∠bOd的平分線垂直,O點到MN的距離為L.MN左側是磁感應強度大小為B、方向豎直向下的勻強磁場.一輕彈簧右端固定,其軸線與∠bOd的平分線重合,自然伸長時左端恰在O點.一質量為m的導體棒ef平行于MN置于導軌上,導體棒與導軌接觸良好.某時刻使導體棒從MN的右側
如圖所示,“×”型光滑金屬導軌abcd固定在絕緣水平面上,ab和cd足夠長,∠aOc=60°.虛線MN與∠bOd的平分線垂直,O點到MN的距離為L.MN左側是磁感應強度大小為B、方向豎直向下的勻強磁場.一輕彈簧右端固定,其軸線與∠bOd的平分線重合,自然伸長時左端恰在O點.一質量為m的導體棒ef平行于MN置于導軌上,導體棒與導軌接觸良好.某時刻使導體棒從MN的右側| L |
| 4 |
| 1 |
| 2 |
 計算,k為彈簧的勁度系數,x為彈簧的形變量。
計算,k為彈簧的勁度系數,x為彈簧的形變量。 
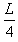 處由靜止開始釋放,導體棒在壓縮彈簧的作用下向左運動,當導體棒運動到O點時彈簧與導體棒分離,導體棒由MN運動到O點的過程中做勻速直線運動,導體棒始終與MN平行。已知導體棒與彈簧彼此絕緣,導體棒和導軌單位長度的電阻均為r0,彈簧被壓縮后所獲得的彈性勢能可用公式Ep=
處由靜止開始釋放,導體棒在壓縮彈簧的作用下向左運動,當導體棒運動到O點時彈簧與導體棒分離,導體棒由MN運動到O點的過程中做勻速直線運動,導體棒始終與MN平行。已知導體棒與彈簧彼此絕緣,導體棒和導軌單位長度的電阻均為r0,彈簧被壓縮后所獲得的彈性勢能可用公式Ep= kx2計算,k為彈簧的勁度系數,x為彈簧的形變量。
kx2計算,k為彈簧的勁度系數,x為彈簧的形變量。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com