
2009年云南省曲靖一中高考沖刺卷理科數學(四)

本試卷分第Ⅰ卷(選擇題)和第Ⅱ卷(非選擇題)兩部分,滿分150分,考試時間120分鐘.
第Ⅰ卷(選擇題,共60分)
一、選擇題:本大題共12小題,每小題5分,共60分.在每小題給出的四個選項中,只
有一項是符合題目要求的.
1.設全集 ,則
,則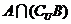 是
是
A.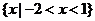 B.
B.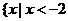 或
或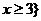

C. D.
D.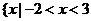 且
且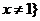

2.己知復數 滿足
滿足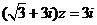 ,則
,則 等于
等于
A.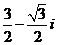 B.
B.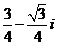 C.
C. D.
D.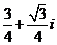

3.設等差數列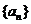 的前
的前 項和為
項和為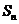 ,若
,若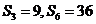 ,則
,則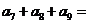

A.63 B.
4.設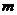 、
、 是不同的直線,
是不同的直線,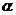 、
、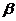 、
、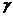 是不同的平面,有以下四個命題:
是不同的平面,有以下四個命題:
① 若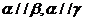 ,則
,則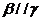 ② 若
② 若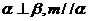 ,則
,則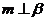

③ 若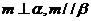 ,則
,則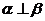 ④ 若
④ 若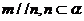 ,則
,則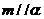

其中真命題的序號是
A.①④ B.②③ C.②④ D.①③
5.已知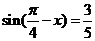 ,則
,則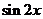 的值為
的值為
A.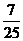 B.
B.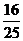 C.
C. D.
D.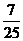

6.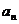 是
是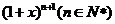 的展開式中含
的展開式中含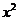 的項的系數,則
的項的系數,則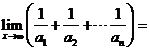

A.1 B.2 C.3 D.4
7.設雙曲線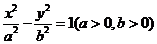 的離心率為
的離心率為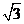 ,且它的一條準線與拋物線
,且它的一條準線與拋物線 的
的
準線重合,則此雙曲線的方程為
A.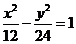 B.
B.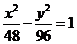 C.
C.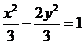 D.
D.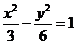

8.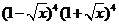 的展開式中
的展開式中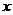 的系數是
的系數是
A.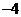 B.
B.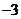 C.3 D.4
C.3 D.4
9.從4名男生和3名女生中選出3人,分別從事三項不同的工作,若這3人中有且只有1
名女生,則選派方案共有
A.108種 B.186種 C.216種 D.270種
10.已知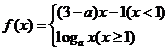 是
是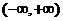 上的增函數,那么
上的增函數,那么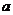 的取值范圍是
的取值范圍是
A.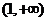 B.
B.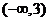 C.
C.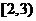 D.(1,3)
D.(1,3)
11.設奇函數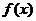 在
在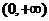 上為增函數,且
上為增函數,且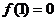 ,則不等式
,則不等式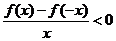 解集
解集
為
A.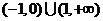 B.
B.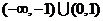

C.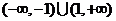 D.
D.

12.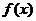 是定義在
是定義在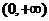 上的非負可導函數,且滿足
上的非負可導函數,且滿足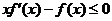 ,對任意正數
,對任意正數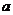 、
、
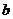 若
若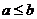 ,則必有
,則必有
A.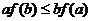 B.
B.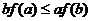

C.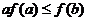 D.
D.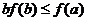


第Ⅱ卷(非選擇題,共90分)
二、填空題:本大題共4小題。每小題5分.共20分.把答案填在題中橫線上.
13.在某項測量中,測量結果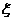 服從正態分布
服從正態分布 ,若
,若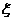 在在(0,1)內取值的 概率為0.4,則
在在(0,1)內取值的 概率為0.4,則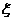 在(0,2)內取值的概率為
.
在(0,2)內取值的概率為
.
14.平面上的向量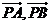 滿足
滿足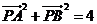 ,且
,且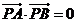 ,若向量
,若向量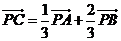 ,
,
則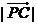 的最大值為
。
的最大值為
。
15.在正方體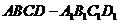 中,
中,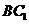 與平面
與平面 所成的角為
.
所成的角為
.
16.給出下列3個命題:
① 命題“存在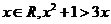 ”的否定是“任意
”的否定是“任意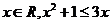 ”;
”;
② “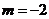 ”是“直線
”是“直線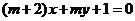 與直線
與直線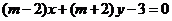 相互垂直”的必要不充分條件;
相互垂直”的必要不充分條件;
③ 關于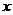 的不等式
的不等式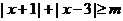 的解集為
的解集為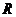 ,則
,則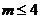 .
.
其中為真命題的序號是
.
三、解答題:本大題共6小題。共70分.解答應寫出文宇說明、證明過程或演算步驟.
17.(本小題滿分12分)
已知函數 的最小正周期為
的最小正周期為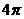 .
.
(1)求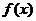 的單調遞增區間;
的單調遞增區間;
(2)在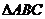 中,角
中,角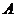 ,
,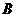 ,
,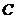 的對邊長分別是
的對邊長分別是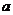 ,
,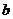 ,
,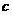 滿足
滿足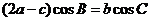 ,求函數
,求函數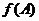 的取值范圍.
的取值范圍.










18.(本小題滿分12分)
有編號為l,2,3,…, 的
的 個學生,入坐編號為1,2,3,…,
個學生,入坐編號為1,2,3,…, 的
的 個座位.每個學生規定坐一個座位,設學生所坐的座位號與該生的編號不同的學生人數為
個座位.每個學生規定坐一個座位,設學生所坐的座位號與該生的編號不同的學生人數為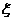 ,已知
,已知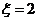 時,共有6種坐法.
時,共有6種坐法.
(1)求 的值;
的值;
(2)求隨機變量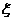 的概率分布列和數學期望.
的概率分布列和數學期望.




19.(本小題滿分12分)
已知數列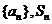 是其前
是其前 項和,且
項和,且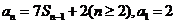 .
.
(1)求數列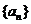 的通項公式;
的通項公式;
(2)設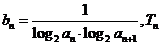 是數列
是數列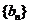 的前
的前 項和,求使得
項和,求使得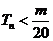 對所有
對所有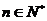 都成立的最小正整數
都成立的最小正整數 。
。






20.(本小題滿分12分)
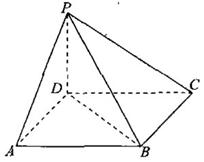 已知四棱錐
已知四棱錐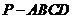 的底面
的底面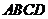 是正方形,且
是正方形,且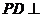 底面
底面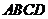 ,其中
,其中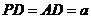 .
.
(1)求二面角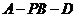 的大小;
的大小;
(2)在線段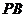 上是否存在一點
上是否存在一點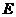 ,使
,使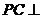 平面
平面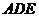 .若存在,試確定
.若存在,試確定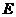 點的位置;若不存在,請說明理由.
點的位置;若不存在,請說明理由.



21.(本小題滿分10分)
已知橢圓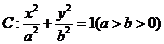 ,過焦點垂直于長軸的弦長為l,且焦點與短軸兩端點構成等邊三角形.
,過焦點垂直于長軸的弦長為l,且焦點與短軸兩端點構成等邊三角形.
(1)求橢圓的方程;
(2)過點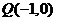 的直線
的直線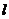 交橢圓于
交橢圓于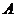 ,
,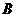 兩點,交直線
兩點,交直線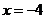 于點
于點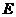 ,點
,點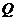 分
分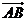 所成比為
所成比為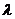 ,點
,點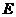 分
分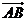 所成比為
所成比為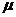 ,求證
,求證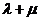 為定值,并計算出該定值.
為定值,并計算出該定值.




22.(本小題滿分12分)
已知函數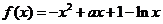 .
.
(1)若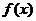 在
在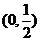 上是減函數,求
上是減函數,求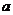 的取值范圍;
的取值范圍;
(2)函數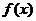 是否既有極大值又有極小值?若存在,求
是否既有極大值又有極小值?若存在,求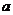 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
一、
1.C 2.D 3.B 4.D 5.D 6.B 7.D 8.A 9.A 10.C
11.D 12.A
1~11.略
12.解: ,
,
 在
在 是減函數,由
是減函數,由 ,得
,得 ,
, ,故選A.
,故選A.
二、
13.0.8 14. 15.
15. 16.①③
16.①③
三、
17.解:(1)

 的單調遞增區間為
的單調遞增區間為
(2)




18.解:(1)當 時,有
時,有 種坐法,
種坐法,
 ,即
,即 ,
,
 或
或 舍去.
舍去. 
(2) 的可能取值是0,2,3,4
的可能取值是0,2,3,4
又

 的概率分布列為
的概率分布列為

0
2
3
4





則 .
.
19.解:(1) 時,
時, ,
,

又
 ,
,

 是一個以2為首項,8為公比的等比數列
是一個以2為首項,8為公比的等比數列

(2)

 最小正整數
最小正整數 .
.
20.解法一:
(1)設 交
交 于點
于點
 平面
平面 .
.
作 于點
于點 ,連接
,連接 ,則由三垂線定理知:
,則由三垂線定理知: 是二面角
是二面角 的平面角.
的平面角.
由已知得 ,
,
 ,
,
∴二面角 的大小的60°.
的大小的60°.
(2)當 是
是 中點時,有
中點時,有 平面
平面 .
.
證明:取 的中點
的中點 ,連接
,連接 、
、 ,則
,則 ,
,
 ,故平面
,故平面 即平面
即平面 .
.
 又
又 平面
平面 ,
,
 平面
平面 .
.
解法二:由已知條件,以 為原點,以
為原點,以 、
、 、
、 為
為 軸、
軸、 軸、
軸、 軸建立空間直角坐標系,則
軸建立空間直角坐標系,則


(1) ,
,
 ,設平面
,設平面 的一個法向量為
的一個法向量為 ,
,
則 取
取
設平面 的一個法向量為
的一個法向量為 ,則
,則 取
取 .
.
 二面角
二面角 的大小為60°.
的大小為60°.
(2)令 ,則
,則 ,
,
 ,
,
由已知, ,要使
,要使 平面
平面 ,只需
,只需 ,即
,即
則有 ,得
,得 當
當 是
是 中點時,有
中點時,有 平面
平面 .
.
21.解:(1)由條件得 ,所以橢圓方程是
,所以橢圓方程是 .
.

(2)易知直線 斜率存在,令
斜率存在,令
由


由 ,
,
即 得
得
 ,
,
即
得

將 代入
代入
有
22.解:(1)
 在
在 上為減函數,
上為減函數, 時,
時, 恒成立,
恒成立,
即 恒成立,設
恒成立,設 ,則
,則
 時,
時, 在(0,
在(0, )上遞減速,
)上遞減速,

 .
.
(2)若 即有極大值又有極小值,則首先必需
即有極大值又有極小值,則首先必需 有兩個不同正要
有兩個不同正要 ,
, ,
,
即 有兩個不同正根
有兩個不同正根
令
∴當 時,
時, 有兩個不同正根
有兩個不同正根
不妨設 ,由
,由 知,
知,
 時,
時, 時,
時, 時,
時,
∴當 時,
時, 既有極大值
既有極大值 又有極小值
又有極小值 .www.ks5u.com
.www.ks5u.com
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com