
2007年臨沂市費縣初中調研考試
八年級數學試題
一、選擇題(本題共15小題,每小題3分,共45分)
1.下列函數中,y是x的正比例函數的是
A.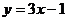 B.
B. C.
C. D.
D.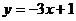
2.在扇形統計圖中,某部分占總體的百分比為25%,則該部分所對的扇形圓心角為
A.120 ° B 90° C.60° D.50°
3.如圖,O是AC、BD的中點,如果兩個全等三角形為一組,那么全等三角形的組數是

A.1
B.
4.下列圖形中,不是軸對稱圖形的是
A.等邊三角形 B.等腰三角形 C.不等邊三角形 D.線段
5.下列計算錯誤的是
A.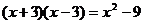 B.
B.
C.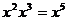 D.
D.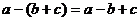
6.把分式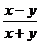 中的x、y都擴大5倍,則分式的值
中的x、y都擴大5倍,則分式的值
A.擴大25倍
B.擴大5倍 C.不變
D.縮小到原來的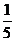
7.化簡 的結果是
的結果是
A.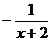 B.
B.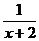 C.
C.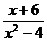 D.
D.
8.下列命題正確的是
A.等腰梯形的對角線相等且互相平分
B.一邊上的兩個角相等的梯形是等腰梯形
C.對角線相等且互相垂直的四邊形是矩形
D.既是矩形,又是菱形的四邊形是正方形
9.已知反比例函數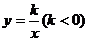 的圖象上有兩點A(
的圖象上有兩點A(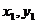 ),B(
),B( ),且
),且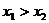 ,則
,則 的值是
的值是
A.正數 B.負數 C.非正數 D.不能確定
10.已知直角三角形的三邊分別是3,4,x,則以x為邊長的正方形的面積是
A.25
B.
11.三角形的三邊長為a,b,c,且滿足(a+b)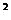 一c
一c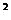 =2ab,則這個三角形的形狀為
=2ab,則這個三角形的形狀為
A.直角三角形 B.等腰三角形 C.銳角三角形 D.鈍角三角形
12.下列四個等式① ;②
;② ;③
;③ ;④
;④ ,其中正確的個數是
,其中正確的個數是
A.0
B.
13.在數學活動課上,王老師和同學們判斷一個四邊形門框是否為矩形,下面是某合作學習小組的4位同學擬定的方案,其中正確的是
A.測量對角線是否相等 B.測量兩組對邊是否分別相等
C.測量一組對角是否都為直角 D.測量其中三個角是否都為直角
14.某校五個綠化小組一天植樹的棵數如下:l0,10,12,x,8,已知這組數據的眾數與平均數相等,那么這組數據的中位數是
A 8
B.
15.一個樣本數據是11個連續的自然數,那么下列結論一定正確的是
A.它的平均數是6 B.它的中位數是6
C.它的方差是5 D.它的方差是10
二、填空題(本題共5小題,每小題3分,共15分)將正確答案直接填在題中橫線上
16.因式分解: .
.
17.當x=
時,分式 有意義.
有意義.
18.已知一個等腰三角形的腰長為
為 .
19.寫出一個圖象位于第一、三象限的反比例函數的解析式 .
20.已知關于x的方程 的解是正數,則m的取值范圍是
.
的解是正數,則m的取值范圍是
.
三、解答題(本題共60分)
21.(8分)為了了解八年級男生的身高情況,現隨機抽取其中一所學校的60名男生(八年級),并對其身高測量后分別制表如下:
分組
147.5―155.5
155.5一l63.5
163.5―l71.5
171.5―179.5
頻數
6
21
a
b
頻率
c
d
e
0.1
測量完,制作好表格后,由于一名同學不小心打翻了一瓶墨汁,污染了表格(標有 a,b,c,d,e的五處被污染,其他三處沒有被污染),調查組準備重新召集這60名男生測一次,小明同學看了看這張污染的表格說:“老師,不用重測了!我可以將這張表格復原。”小明能辦到嗎?a,b,c,d,e分別是什么?
22.(8分)P是等邊三角形ABC內的一點,連接PA、PB、PC,以BP為邊作∠PBQ=60°,且BQ=BP,連接CQ,觀察并猜想AP與CQ之間的大小關系,并證明你的結論.

23.(10分)騎自行車比步行每小時快
24.(10分)水池中有水若干噸,若單開一個出水口,水流速度v與全池水放光所用時間t如下表:
用時t(小時)
10
5

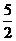
2

1
…… 逐漸減少
逐漸減少
出水速度v
(噸/小時)
l
2
3
4
5
8
10
…… 逐漸增大
逐漸增大
(1)①根據表中的數據在直角坐標系中描出實數對(t,v)的對應點;
②通過描點、連線、猜測、驗證等方法確定v與t之間的函數關系式,并畫出圖象.
③當出水速度為每小時20噸時,多少小時可放完池中的水?
25.(12分)某校要從王聰和李明兩名同學中挑選一人參加全國數學競賽,在最近的五次選拔測試中,他倆的成績分別如下表:

根據上表解答下列問題
(1)完成下表;
姓名
極差(分)
平均分
中位數(分)
眾數(分)
方差
王聰
40
80
75
75
190
李明
(2)在這五次測試中,成績比較穩定的同學是誰?若將80分以上(含80分)的成績視為優秀,則王聰、李明在這五次測試中的優秀率分別是多少?
(3)歷屆比賽表明,成績達到80分以上(含80分)就很可能獲得獎,成績達到90分以上(含90分)就很可能獲得一等獎,那么你認為應選誰參加比賽比較合適?說明你的理由?
26.(12分)如圖,一等腰直角三角尺GEF的兩條直角邊與正方形ABCD的兩條邊分別重合在一起,現正方形ABCD保持不動,將三角尺GEF繞斜邊EF的中點O(點O也是BD中點)按順時針方向旋轉.

(1)如圖2,當EF與AB相交于點M,GF與BD相交于點N時,通過觀察或測量BM、FN的長度,猜想BM、FN滿足的數量關系,并證明你的猜想;
(2)若三角尺GEF旋轉到如圖3所示的位置時,線段FE的延長線與AB的延長線相交于點M,線段BD的延長線與GF延長線相交于點N,此時,(1)中的猜想還成立嗎?若成立,請證明;若不成立,請說明理由.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com