
2009屆高考數(shù)學(xué)第三輪復(fù)習(xí)精編模擬七
參考公式:
如果事件 互斥,那么
球的表面積公式
互斥,那么
球的表面積公式


如果事件 相互獨(dú)立,那么
其中
相互獨(dú)立,那么
其中 表示球的半徑
表示球的半徑
 球的體積公式
球的體積公式
如果事件 在一次試驗(yàn)中發(fā)生的概率是
在一次試驗(yàn)中發(fā)生的概率是 ,那么
,那么

 次獨(dú)立重復(fù)試驗(yàn)中事件
次獨(dú)立重復(fù)試驗(yàn)中事件 恰好發(fā)生
恰好發(fā)生 次的概率
其中
次的概率
其中 表示球的半徑
表示球的半徑

第一部分 選擇題(共50分)
一.選擇題:本大題共10小題,每小題5分,共50分.在每小題給出的四個(gè)選項(xiàng)中,只有一項(xiàng)是符合題目要求的
1、若sin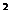 x>cos
x>cos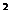 x,則x的取值范圍是(
)w.w.w.k.s.5.u.c.o.m
x,則x的取值范圍是(
)w.w.w.k.s.5.u.c.o.m
(A){x|2k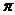 -
-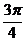 <x<2k
<x<2k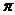 +
+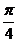 ,k
,k Z} (B) {x|2k
Z} (B) {x|2k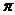 +
+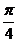 <x<2k
<x<2k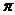 +
+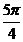 ,k
,k Z}
Z}
(C) {x|k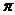 -
-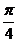 <x<k
<x<k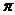 +
+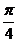 ,k
,k Z } (D) {x|k
Z } (D) {x|k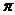 +
+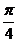 <x<k
<x<k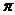 +
+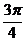 ,k
,k Z}
Z}
2 在復(fù)平面內(nèi),把復(fù)數(shù)3-
在復(fù)平面內(nèi),把復(fù)數(shù)3-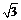 i對(duì)應(yīng)的向量按順時(shí)針?lè)较蛐D(zhuǎn)π/3,所得向量對(duì)應(yīng)的復(fù)數(shù)是…………………………( )w.w.w.k.s.5.u.c.o.m
i對(duì)應(yīng)的向量按順時(shí)針?lè)较蛐D(zhuǎn)π/3,所得向量對(duì)應(yīng)的復(fù)數(shù)是…………………………( )w.w.w.k.s.5.u.c.o.m
 A)2
A)2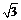 B)-2
B)-2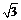 i C)
i C)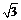 -3i D)3+
-3i D)3+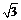 i
i
3、已知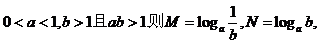
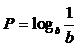 .三數(shù)大小關(guān)系為 ( )
.三數(shù)大小關(guān)系為 ( )
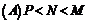
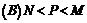
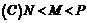
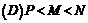
4、若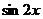 、
、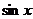 分別是
分別是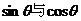 的等差中項(xiàng)和等比中項(xiàng),則
的等差中項(xiàng)和等比中項(xiàng),則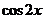 的值為:( )
的值為:( )
 A、
A、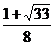 B、
B、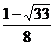 C、
C、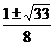 D、
D、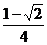
5、方程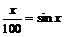 的實(shí)數(shù)解的個(gè)數(shù)為 ( )
的實(shí)數(shù)解的個(gè)數(shù)為 ( )
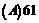
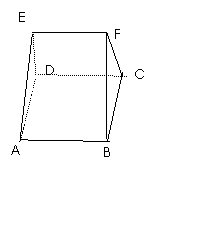
6、如圖,在多面體ABCDEF中,已知面ABCD是邊長(zhǎng)為3的正方形,
EF//AB, EF=3/2,EF與面AC的距離為2,則該多面體的體積為……( )
A)9/2 B)
7、過(guò)拋物線y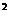 =4x的焦點(diǎn),作直線與此拋物線相交于兩點(diǎn)P和Q,那么線段PQ中點(diǎn)的軌跡方程是(
)
=4x的焦點(diǎn),作直線與此拋物線相交于兩點(diǎn)P和Q,那么線段PQ中點(diǎn)的軌跡方程是(
)
(A) y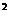 =2x-1
(B) y
=2x-1
(B) y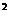 =2x-2
=2x-2
(C) y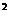 =-2x+1
(D) y
=-2x+1
(D) y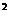 =-2x+2
=-2x+2
8、設(shè)函數(shù)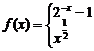
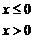 ,若
,若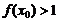 ,則
,則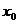 的取值范圍是(
)
的取值范圍是(
)
(A)(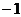 ,1)
(B)(
,1)
(B)(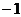 ,
,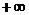 )
)
(C)(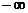 ,
,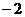 )
)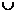 (0,
(0,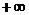 ) (D)(
) (D)(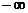 ,
,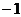 )
)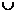 (1,
(1,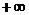 )
)
9、若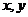 滿足
滿足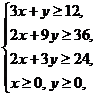 ,則使得
,則使得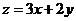 的值最小的
的值最小的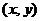 是 ( )
是 ( )
A、(4.5,3) B、(3,6) C、(9,2) D、(6,4)
10、已知兩點(diǎn)M(1,5/4),N(-4,-5/4),給出下列曲線方程:
①4x+2y-1=0 ②x2+y2=3 ③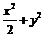 =1 ④
=1 ④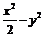 =1
=1
在曲線上存在點(diǎn)P滿足|MP|=|NP|的所有曲線方程是………………………………( )
A)①③ B)②④ C)①②③ D)②③④
第二部分 非選擇題(共100分)
二、填空題:本大題共5小題,其中14~15題是選做題,考生只能選做一題,兩題全答的,只計(jì)算前一題得分.每小題5分,滿分20分.
11、現(xiàn)時(shí)盛行的足球彩票,其規(guī)則如下:全部13場(chǎng)足球比賽,每場(chǎng)比賽有3種結(jié)果:勝、平、負(fù),13長(zhǎng)比賽全部猜中的為特等獎(jiǎng),僅猜中12場(chǎng)為一等獎(jiǎng),其它不設(shè)獎(jiǎng),則某人獲得特等獎(jiǎng)的概率為 。
12、數(shù)列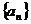 中,
中,
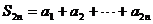 , 則
, 則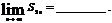
13、一只酒杯的軸截面是拋物線的一部分,它的函數(shù)解析式是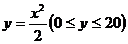 ,在杯內(nèi)放一個(gè)玻璃球,要使球觸及酒杯底部,則玻璃球的半徑r的取值范圍是___________.
,在杯內(nèi)放一個(gè)玻璃球,要使球觸及酒杯底部,則玻璃球的半徑r的取值范圍是___________.
14、(坐標(biāo)系與參數(shù)方程選做題)
已知圓的極坐標(biāo)方程為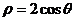 ,則該圓的圓心到直線
,則該圓的圓心到直線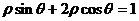 的距離是
.
的距離是
.
15.(幾何證明選講選做題) 已知AB是圓O的直徑,EF切圓O于C,AD⊥EF于D,AD=2,AB=6,則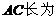 _______.
_______.
三.解答題:本大題共6小題,共80分,解答應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟.
16.(本小題滿分12分)
已知 ,
,
(Ⅰ)求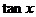 的值;
(Ⅱ)求
的值;
(Ⅱ)求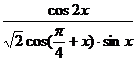 的值.
的值.
17. (本小題滿分12分)
已知函數(shù)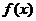 是定義在
是定義在 上的單調(diào)奇函數(shù), 且
上的單調(diào)奇函數(shù), 且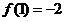 .
.
(Ⅰ)求證函數(shù)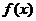 為
為 上的單調(diào)減函數(shù);
上的單調(diào)減函數(shù);
(Ⅱ) 解不等式 .
.
18.(本小題滿分14分)
已知函數(shù)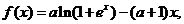 (其中
(其中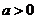 ) ,
) ,
點(diǎn)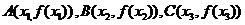 從左到右依次是函數(shù)
從左到右依次是函數(shù)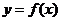 圖象上三點(diǎn),且
圖象上三點(diǎn),且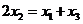 .
.
(Ⅰ) 證明: 函數(shù)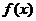 在
在 上是減函數(shù);
上是減函數(shù);
(Ⅱ)
求證:ㄓ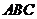 是鈍角三角形;
是鈍角三角形;
(Ⅲ) 試問(wèn),ㄓ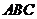 能否是等腰三角形?若能,求ㄓ
能否是等腰三角形?若能,求ㄓ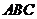 面積的最大值;若不能,請(qǐng)說(shuō)明理由.
面積的最大值;若不能,請(qǐng)說(shuō)明理由.
19.(本小題滿分14分)
已知數(shù)列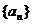 滿足:
滿足: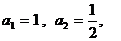 且
且
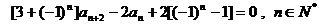 .
.
(Ⅰ)求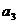 ,
,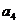 ,
,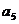 ,
,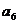 的值及數(shù)列
的值及數(shù)列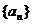 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅱ)設(shè)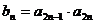 ,求數(shù)列
,求數(shù)列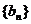 的前
的前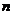 項(xiàng)和
項(xiàng)和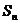 ;
;
20.(本小題滿分14分)
(I)求證: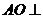 平面BCD;
平面BCD;
(II)求點(diǎn)E到平面ACD的距離;
(III)求二面角A―CD―B的余弦值。
21. (本小題滿分14分)
設(shè)直線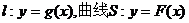 . 若直線l與曲線S同時(shí)滿足下列兩個(gè)條件:①直線l與曲線S相切且至少有兩個(gè)切點(diǎn);②對(duì)任意x∈R都有
. 若直線l與曲線S同時(shí)滿足下列兩個(gè)條件:①直線l與曲線S相切且至少有兩個(gè)切點(diǎn);②對(duì)任意x∈R都有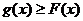 . 則稱直線l為曲線S的“上夾線”.
. 則稱直線l為曲線S的“上夾線”.
(Ⅰ)已知函數(shù)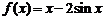 .求證:
.求證: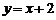 為曲線
為曲線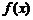 的“上夾線”.
的“上夾線”.
(Ⅱ)觀察下圖:
根據(jù)上圖,試推測(cè)曲線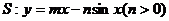 的“上夾線”的方程,并給出證明.
的“上夾線”的方程,并給出證明.
一.選擇題:DBBAC DBDBD
解析:1:由sin x>cos
x>cos x得cos
x得cos x-sin
x-sin x<0, 即cos2x<0,所以:
x<0, 即cos2x<0,所以: +kπ<2x<
+kπ<2x< +kπ,選D.
+kπ,選D.
2:∵復(fù)數(shù)3- i的一個(gè)輻角為-π/6,對(duì)應(yīng)的向量按順時(shí)針?lè)较蛐D(zhuǎn)π/3,
i的一個(gè)輻角為-π/6,對(duì)應(yīng)的向量按順時(shí)針?lè)较蛐D(zhuǎn)π/3,
所得向量對(duì)應(yīng)的輻角為-π/2,此時(shí)復(fù)數(shù)應(yīng)為純虛數(shù),對(duì)照各選擇項(xiàng),選(B)。
3:由 又
又 代入選擇支檢驗(yàn)
代入選擇支檢驗(yàn) 被排除;又由
被排除;又由 ,
, 即
即 被排除.故選
被排除.故選 .
.
4:依題意有 , ①
, ①  ②
②
由①2-②×2得, ,解得
,解得 。
。
又由 ,得
,得 ,所以
,所以 不合題意。故選A。
不合題意。故選A。
5:令 ,這兩個(gè)方程的曲線交點(diǎn)的個(gè)數(shù)就是原方程實(shí)數(shù)解的個(gè)數(shù).由于直線
,這兩個(gè)方程的曲線交點(diǎn)的個(gè)數(shù)就是原方程實(shí)數(shù)解的個(gè)數(shù).由于直線 的斜率為
的斜率為 ,又
,又 所以僅當(dāng)
所以僅當(dāng) 時(shí),兩圖象有交點(diǎn).由函數(shù)
時(shí),兩圖象有交點(diǎn).由函數(shù) 的周期性,把閉區(qū)間
的周期性,把閉區(qū)間 分成
分成


 共
共 個(gè)區(qū)間,在每個(gè)區(qū)間上,兩圖象都有兩個(gè)交點(diǎn),注意到原點(diǎn)多計(jì)一次,故實(shí)際交點(diǎn)有
個(gè)區(qū)間,在每個(gè)區(qū)間上,兩圖象都有兩個(gè)交點(diǎn),注意到原點(diǎn)多計(jì)一次,故實(shí)際交點(diǎn)有 個(gè).即原方程有63個(gè)實(shí)數(shù)解.故選
個(gè).即原方程有63個(gè)實(shí)數(shù)解.故選 .
.
6:連接BE、CE則四棱錐E-ABCD的體積VE-ABCD= ×3×3×2=6,又整個(gè)幾何體大于部分的體積,所求幾何體的體積V求> VE-ABCD,選(D)
×3×3×2=6,又整個(gè)幾何體大于部分的體積,所求幾何體的體積V求> VE-ABCD,選(D)