
2009屆高考數學第三輪復習精編模擬四
參考公式:
如果事件 互斥,那么
球的表面積公式
互斥,那么
球的表面積公式


如果事件 相互獨立,那么
其中
相互獨立,那么
其中 表示球的半徑
表示球的半徑
 球的體積公式
球的體積公式
如果事件 在一次試驗中發生的概率是
在一次試驗中發生的概率是 ,那么
,那么

 次獨立重復試驗中事件
次獨立重復試驗中事件 恰好發生
恰好發生 次的概率
其中
次的概率
其中 表示球的半徑
表示球的半徑

第一部分 選擇題(共50分)
一.選擇題:本大題共10小題,每小題5分,共50分.在每小題給出的四個選項中,只有一項是符合題目要求的
1、設復數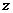 滿足關系式
滿足關系式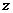 +│
+│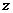 │=2+
│=2+ ,那么
,那么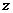 等于( )
w.w.w.k.s.5.u.c.o.m
等于( )
w.w.w.k.s.5.u.c.o.m
(A) - +
+ ;(B)
;(B)  -
- ;(C) -
;(C) - -
- ; (D)
; (D)  +
+ .
.
2 設函數
設函數 為 ( )
為 ( )
 A.周期函數,最小正周期為
A.周期函數,最小正周期為 B.周期函數,最小正周期為
B.周期函數,最小正周期為
C.周期函數,數小正周期為 D.非周期函數
D.非周期函數
3、設 則以下不等式中不恒成立的是 ( )
則以下不等式中不恒成立的是 ( )
A. ; B.
; B. ;
;
C. ; D.
; D.
4、如果 的展開式中各項系數之和為128,則展開式中的系數是( )
的展開式中各項系數之和為128,則展開式中的系數是( )
(A)7 (B)-7 (C)21 (D)-21
5、若直線 與直線
與直線 的交點位于第一象限,則直線
的交點位于第一象限,則直線 的傾斜角的取值范圍是 ( )
的傾斜角的取值范圍是 ( )
(A) , (B)
, (B) ,
,
(C)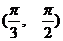 , (D)
, (D)
6、 如果 ,
, ,…,
,…, 為各項都大于零的等差數列,公差
為各項都大于零的等差數列,公差 ,則
,則
(A)


 ;(B)
;(B)


 ;(C)
;(C) +
+

 +
+ ;(D)
;(D)
 =
= .
.
7、設三棱柱ABC―A1B
A. B.
B. C.
C. D.
D.
 8、函數
8、函數 的部分圖象如圖,則( )
的部分圖象如圖,則( )
A. ; B.
; B. ;
;
C. ; D.
; D.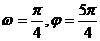
9、若橢圓經過原點,且焦點F1(1,0),F2(3,0),則其離心率為 ( )
A、 B、
B、 C、
C、 D、
D、
10、《中華人民共和國個人所得稅法》規定,公民全月工資、薪金所得不超過800元的部分不必納稅,超過800元的部分為全月應納稅所得額.此項稅款按下表分段累進計算:
全月應納稅所得額
稅率
不超過500元的部分
5%
超過500元至2000元的部分
10%
超過2000元至5000元的部分
15%
……
…
某人一月份應交納此項稅款26.78元,則他的當月工資、薪金所得介于
 800~900元
800~900元
 900~1200元
900~1200元
 1200~1500元
1200~1500元
 1500~2800元
1500~2800元
第二部分 非選擇題(共100分)
二、填空題:本大題共5小題,其中14~15題是選做題,考生只能選做一題,兩題全答的,只計算前一題得分.每小題5分,滿分20分.
11、已知集合為 ,它的所有的三個元素的子集的和是
,它的所有的三個元素的子集的和是 ,則
,則 =
。
=
。
12、若函數 上為增函數,則實數a、b的取值范圍是___________;
上為增函數,則實數a、b的取值范圍是___________;
13、橢圓 的焦點為
的焦點為 ,點P為其上的動點,當
,點P為其上的動點,當 為鈍角時,點P橫坐標的取值范圍是_______________________;
為鈍角時,點P橫坐標的取值范圍是_______________________;
 14、(坐標系與參數方程選做題) 極坐標系中,曲線
14、(坐標系與參數方程選做題) 極坐標系中,曲線 和
和 相交于點
相交于點 ,則
,則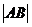 =
;
=
;
15.(幾何證明選講選做題) 如圖:PA與圓O相切于A,PCB為圓O的割線,
并且不過圓心O,已知∠BPA= , PA=
, PA= ,PC=1,
,PC=1,
則圓O的半徑等于 .
三.解答題:本大題共6小題,共80分,解答應寫出文字說明、證明過程或演算步驟.
16.(本小題滿分12分)
已知:復數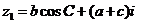 ,
, ,且
,且 ,其中
,其中 、
、 為△ABC的內角,
為△ABC的內角, 、
、 、
、 為角
為角 、
、 、
、 所對的邊.
所對的邊.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ) 若 ,求△ABC的面積.
,求△ABC的面積.
17.(本小題滿分12分)
某次有獎競猜活動中,主持人準備了A、B兩個相互獨立的問題, 并且宣布:觀眾答對問題A可獲獎金 元,答對問題B可獲獎金2
元,答對問題B可獲獎金2 元;先答哪個題由觀眾自由選擇;只有第一個問題答對,才能再答第二個問題,否則終止答題.設某幸運觀眾答對問題A、B的概率分別為
元;先答哪個題由觀眾自由選擇;只有第一個問題答對,才能再答第二個問題,否則終止答題.設某幸運觀眾答對問題A、B的概率分別為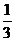 、
、 .你覺得他應先回答哪個問題才能使獲得獎金的期望較大?說明理由.
.你覺得他應先回答哪個問題才能使獲得獎金的期望較大?說明理由.
18.(本小題滿分14分)
在以O為原點的直角坐標系中,點A(4,-3)為△OAB的直角頂點,已知|AB|=2|OA|,且點B的縱坐標大于0。
(Ⅰ)求 的坐標;
的坐標;
(Ⅱ)求圓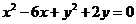 關于直線OB對稱的圓的方程。
關于直線OB對稱的圓的方程。
19.(本小題滿分14分)
已知函數f(x)的定義域為R,對任意的 ,且當
,且當 時,
時, .
.
(Ⅰ)求證:函數f(x)為奇函數;
(Ⅱ)求證:
(Ⅲ)求函數 在區間[-n,n](n
在區間[-n,n](n )上的最大值和最小值。
)上的最大值和最小值。
20.(本小題滿分14分)
如圖,已知三棱柱ABC-A1B
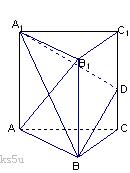 B沿棱柱側面經過棱C C1到點A1的最短路線長為
B沿棱柱側面經過棱C C1到點A1的最短路線長為 ,設這條最短路線與CC1的交
,設這條最短路線與CC1的交
點為D.
(1)求三棱柱ABC-A1B
(2)在平面A1BD內是否存在過點D的直線與平面ABC平行?證明你的判斷;
(3)證明:平面A1BD⊥平面A1ABB1.
2. (本小題滿分14分)
已知函數
(Ⅰ)若函數y=f(x)的圖象切x軸于點(2,0),求a、b的值;
(Ⅱ)設函數y=f(x)  的圖象上任意一點的切線斜率為k,試求
的圖象上任意一點的切線斜率為k,試求 的充要條件;
的充要條件;
(Ⅲ)若函數y=f(x)的圖象上任意不同的兩點的連線的斜率小于1,求證 。
。
一.選擇題:DBBCB BCCCC
解析:1:因為 =(2 -│
=(2 -│ │)+
│)+  ,由選擇支知│
,由選擇支知│ │<2,所以
│<2,所以 的實部為正數,虛部為1,根據這個隱含條件,(A),(B),(C)均可篩去,所以選(D).
的實部為正數,虛部為1,根據這個隱含條件,(A),(B),(C)均可篩去,所以選(D).
2:先將周期最小的選項(A)的周期T= 代入
代入 檢驗,不成立則排除(A);再檢驗(B)成立. 所以選(B).
檢驗,不成立則排除(A);再檢驗(B)成立. 所以選(B).
3:∵ ∴可取
∴可取 代入四個選項驗證,發現B錯誤,∴應選(B).
代入四個選項驗證,發現B錯誤,∴應選(B).
4:“ 的展開式中各項系數之和為
的展開式中各項系數之和為
由通項公式Tr+1= =
= ,
,
令7-=-3,解得r=6,此時T7= ,故選C

5:作兩直線的圖象,從圖中可以看出:
直線 的傾斜角的取值范圍應選(B).
的傾斜角的取值范圍應選(B).
6:取特殊數列 =
= ,排除(A)、(C)、(D). ∴選(B).
,排除(A)、(C)、(D). ∴選(B).
7:如圖所示,
作
∴柱體體積

 故選C.
故選C.
8:由圖象可知,x=1時 =1. 由此可排除(A)、(D);再由周期T=8,可排除(B).
=1. 由此可排除(A)、(D);再由周期T=8,可排除(B).
∴應選(C).
9:利用橢圓的定義可得 故離心率
故離心率 故選C。
故選C。
10:設某人當月工資為1200元或1500元,則其應納稅款分別為:400 5%=20元,500
5%=20元,500 5%+200
5%+200 10%=45元,可排除
10%=45元,可排除 、
、 、
、 .故選
.故選 .
.
二.填空題:11、2; 12、a>0且 ;13、
;13、 ;14、
;14、 ;15、7;
;15、7;
解析:11:因為包含了 任意一個元素
任意一個元素 的三元素集合共
的三元素集合共 個,所以在
個,所以在 中,每個元素都出現了
中,每個元素都出現了 次,所以
次,所以

 ,所以
,所以
 。
。
12:由已知可畫出下圖,符合題設,故a>0且 。
。
13:設P(x,y),則當 時,點P的軌跡為
時,點P的軌跡為 ,由此可得點P的橫坐標
,由此可得點P的橫坐標 。
。
又當P在x軸上時, ,點P在y軸上時,
,點P在y軸上時, 為鈍角,由此可得點P橫坐標的取值范圍是:
為鈍角,由此可得點P橫坐標的取值范圍是: ;
;
 14.解:在平面直角坐標系中,曲線
14.解:在平面直角坐標系中,曲線 和
和 分別表示圓
分別表示圓 和直線
和直線 ,易知
,易知 =
=
15.解:  由圓的性質PA
由圓的性質PA =PC?PB,得,PB=12,連接OA并反向延長
=PC?PB,得,PB=12,連接OA并反向延長
交圓于點E,在直角三角形APD中可以求得PD=4,DA=2,故CD=3,
DB=8,J記圓的半徑為R,由于ED?DA=CD?DB
因此,(2R-2) ?2=3?8,解得R=7
三.解答題:
16.解:(Ⅰ)∵ ∴
∴ ----①,
----①, ----②
----②
由①得 ------③
------③
在△ABC中,由正弦定理得 =
= ,設
,設
 =
=
則 ,代入③得
,代入③得

∵  ∴
∴ ∴
∴ ,∵
,∵ ∴
∴ ……………………6分
……………………6分
(Ⅱ) ∵ ,由余弦定理得
,由余弦定理得

 ,--④
,--④
由②得 -⑤ 由④⑤得
-⑤ 由④⑤得 ,∴
,∴ =
= . ……………………………12分
. ……………………………12分
17.解:設該觀眾先答A題所獲獎金為 元,先答B題所獲獎金為
元,先答B題所獲獎金為 元,………………………1分
元,………………………1分
依題意可得 可能取的值為:0,
可能取的值為:0,  ,3
,3 ,
,  的可能取值為:0,2
的可能取值為:0,2 ,3
,3
………………………2分
∵ ,
, ,
, ,
,
∴ ,
………………………6分
,
………………………6分
∵ ,
, ,
, 
∴ ………………………10分
………………………10分
∵
 ∴
∴ ,即
,即
∴該觀眾應先回答B題所獲獎金的期望較大. ……………………………12分
18.解:(Ⅰ)設 ,由
,由 得
得 ,解得
,解得 或
或 ,若
,若 則
則 與
與 矛盾,所以
矛盾,所以 不合舍去。
不合舍去。
即 。---------------------------------------------------------------------------6
。---------------------------------------------------------------------------6
(Ⅱ)圓 即
即 ,其圓心為C(3,-1),半徑
,其圓心為C(3,-1),半徑 ,
,
∴直線OB的方程為 ,-----------------------------------------------------------------10
,-----------------------------------------------------------------10
設圓心C(3,-1)關于直線 的對稱點的坐標為(a,b),則
的對稱點的坐標為(a,b),則

解得: ,則所求的圓的方程為
,則所求的圓的方程為 。-----------------------------14
。-----------------------------14
19.(Ⅰ)證明:∵對任意的 ①
①
令 得
得 ②…………1分
②…………1分
令 得
得 ……………………2分
……………………2分
∴ 由②得
由②得
∴函數 為奇函數………………………………3分
為奇函數………………………………3分
(Ⅱ)證明:(1)當n=1時等式顯然成立
(2)假設當n=k(k )時等式成立,即
)時等式成立,即 ,…………4分
,…………4分
則當n=k+1時有
 ,由①得
,由①得 ………………6分
………………6分
∵ ∴
∴
∴當n=k+1時,等式成立。
綜(1)、(2)知對任意的 ,
, 成立。………………8分
成立。………………8分
(Ⅲ)解:設 ,因函數
,因函數 為奇函數,結合①得
為奇函數,結合①得
 =
= ,……………………9分
,……………………9分
∵
又∵當 時,
時,
∴
 ,∴
,∴
∴函數 在R上單調遞減…………………………………………12分
在R上單調遞減…………………………………………12分
∴

由(2)的結論得 ,
,
∵ ,∴
,∴ =-2n
=-2n
∵函數 為奇函數,∴
為奇函數,∴
∴
 ,
, =2n。……………………14分
=2n。……………………14分
20.解:(1)如圖,將側面BB
∵CD∥AA1 ∴D為CC1的中點,……………………………2分
在Rt△A1AB2中,由勾股定理得 ,
,
即 解得
解得 ,……………………4分
,……………………4分
∵ ∴
∴ ……………………………………6分
……………………………………6分
(2)設A1B與AB1的交點為O,連結BB2,OD,則 ……………………………7分
……………………………7分
∵ 平面
平面 ,
, 平面
平面 ∴
∴ 平面
平面 ,
,
即在平面A1BD內存在過點D的直線與平面ABC平行 ……………………………9分
(3)連結AD,B1D ∵ ≌
≌ ≌
≌
∴ ∴
∴ ……………………………11分
……………………………11分
∵ ∴
∴ 平面A1ABB1 ……………………………13分
平面A1ABB1 ……………………………13分
又∵ 平面A1BD ∴平面A1BD⊥平面A1ABB1 ……………………………………14分
平面A1BD ∴平面A1BD⊥平面A1ABB1 ……………………………………14分
21.解:(Ⅰ)
 …………………………………………1分
…………………………………………1分
由 得
得 , ………………………………………………2分
, ………………………………………………2分
又 得
得 ……………………………………………………3分
……………………………………………………3分
(Ⅱ) k=
k=
 ,
,
 對任意的
對任意的
 ,即
,即 對任意的
對任意的 恒成立……4分
恒成立……4分
等價于 對任意的
對任意的 恒成立。…………………………5分
恒成立。…………………………5分
令g(x)= ,h(x)=
,h(x)= ,
,
則 ,
, …………………………………………6分
…………………………………………6分
 ,當且僅當
,當且僅當 時“=”成立,
時“=”成立,
 …………7分
…………7分
 h(x)=
h(x)= 在(0,1)上為增函數,
在(0,1)上為增函數, h(x)max<2……………………………8分
h(x)max<2……………………………8分

 ……………………………………………………………………9分
……………………………………………………………………9分
(Ⅲ)設 則
則 =
= ……10分
……10分
即 ,對
,對 恒成立…………………………11分
恒成立…………………………11分

 ,對
,對 恒成立
恒成立
即 對
對 恒成立…………………………13分
恒成立…………………………13分


解得 ……………………………………………………14分
……………………………………………………14分
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com