
題目列表(包括答案和解析)
(幾何證明選講選做題) 如圖:PA與圓O相切于A,PCB為圓O的割線,并且不過圓心O,已知∠BPA=![]() , PA=
, PA=![]() ,PC=1,則圓O的半徑等于 .
,PC=1,則圓O的半徑等于 .

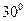 , PA=
, PA=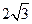 ,PC=1,則圓O的半徑等于 .
,PC=1,則圓O的半徑等于 .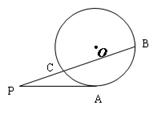
(幾何證明選講選做題) 如圖:PA與圓O相切于A,
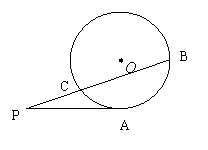 PCB為圓O的割線,并且不過圓心O,已知
PCB為圓O的割線,并且不過圓心O,已知![]() ∠BPA=
∠BPA=![]() ,
,
PA=![]() ,PC=1,則圓O的半徑等于 .
,PC=1,則圓O的半徑等于 .
(幾何證明選講選做題) 如圖:PA與圓O相切于A,
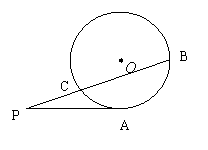 PCB為圓O的割線,并且不過圓心O,已知
PCB為圓O的割線,并且不過圓心O,已知![]() ∠BPA=
∠BPA=![]() ,
,
PA=![]() ,PC=1,則圓O的半徑等于 .
,PC=1,則圓O的半徑等于 .
(幾何證明選講選做題)如圖:已知PA是圓O的切線,切點(diǎn)為A,PA=2. AC是圓O的直徑,PC與圓O交于點(diǎn)B,PB=1,
則圓O的半徑R=_____ _.
一.選擇題:DBBCB BCCCC
解析:1:因?yàn)?sub> =(2 -│
=(2 -│ │)+
│)+  ,由選擇支知│
,由選擇支知│ │<2,所以
│<2,所以 的實(shí)部為正數(shù),虛部為1,根據(jù)這個(gè)隱含條件,(A),(B),(C)均可篩去,所以選(D).
的實(shí)部為正數(shù),虛部為1,根據(jù)這個(gè)隱含條件,(A),(B),(C)均可篩去,所以選(D).
2:先將周期最小的選項(xiàng)(A)的周期T= 代入
代入 檢驗(yàn),不成立則排除(A);再檢驗(yàn)(B)成立. 所以選(B).
檢驗(yàn),不成立則排除(A);再檢驗(yàn)(B)成立. 所以選(B).
3:∵ ∴可取
∴可取 代入四個(gè)選項(xiàng)驗(yàn)證,發(fā)現(xiàn)B錯(cuò)誤,∴應(yīng)選(B).
代入四個(gè)選項(xiàng)驗(yàn)證,發(fā)現(xiàn)B錯(cuò)誤,∴應(yīng)選(B).
4:“ 的展開式中各項(xiàng)系數(shù)之和為
的展開式中各項(xiàng)系數(shù)之和為
由通項(xiàng)公式Tr+1= =
= ,
,
令7-=-3,解得r=6,此時(shí)T7= ,故選C

5:作兩直線的圖象,從圖中可以看出:
直線 的傾斜角的取值范圍應(yīng)選(B).
的傾斜角的取值范圍應(yīng)選(B).
6:取特殊數(shù)列 =
= ,排除(A)、(C)、(D). ∴選(B).
,排除(A)、(C)、(D). ∴選(B).
7:如圖所示,
作
∴柱體體積

 故選C.
故選C.
8:由圖象可知,x=1時(shí) =1. 由此可排除(A)、(D);再由周期T=8,可排除(B).
=1. 由此可排除(A)、(D);再由周期T=8,可排除(B).
∴應(yīng)選(C).
9:利用橢圓的定義可得 故離心率
故離心率 故選C。
故選C。
10:設(shè)某人當(dāng)月工資為1200元或1500元,則其應(yīng)納稅款分別為:400 5%=20元,500
5%=20元,500 5%+200
5%+200 10%=45元,可排除
10%=45元,可排除 、
、 、
、 .故選
.故選 .
.
二.填空題:11、2; 12、a>0且 ;13、
;13、 ;14、
;14、 ;15、7;
;15、7;
解析:11:因?yàn)榘?sub> 任意一個(gè)元素
任意一個(gè)元素 的三元素集合共
的三元素集合共 個(gè),所以在
個(gè),所以在 中,每個(gè)元素都出現(xiàn)了
中,每個(gè)元素都出現(xiàn)了 次,所以
次,所以

 ,所以
,所以
 。
。
12:由已知可畫出下圖,符合題設(shè),故a>0且 。
。
13:設(shè)P(x,y),則當(dāng) 時(shí),點(diǎn)P的軌跡為
時(shí),點(diǎn)P的軌跡為 ,由此可得點(diǎn)P的橫坐標(biāo)
,由此可得點(diǎn)P的橫坐標(biāo) 。
。
又當(dāng)P在x軸上時(shí), ,點(diǎn)P在y軸上時(shí),
,點(diǎn)P在y軸上時(shí), 為鈍角,由此可得點(diǎn)P橫坐標(biāo)的取值范圍是:
為鈍角,由此可得點(diǎn)P橫坐標(biāo)的取值范圍是: ;
;
 14.解:在平面直角坐標(biāo)系中,曲線
14.解:在平面直角坐標(biāo)系中,曲線 和
和 分別表示圓
分別表示圓 和直線
和直線 ,易知
,易知 =
=
15.解:  由圓的性質(zhì)PA
由圓的性質(zhì)PA =PC?PB,得,PB=12,連接OA并反向延長(zhǎng)
=PC?PB,得,PB=12,連接OA并反向延長(zhǎng)
交圓于點(diǎn)E,在直角三角形APD中可以求得PD=4,DA=2,故CD=3,
DB=8,J記圓的半徑為R,由于ED?DA=CD?DB
因此,(2R-2) ?2=3?8,解得R=7
三.解答題:
16.解:(Ⅰ)∵ ∴
∴ ----①,
----①, ----②
----②
由①得 ------③
------③
在△ABC中,由正弦定理得 =
= ,設(shè)
,設(shè)
 =
=
則 ,代入③得
,代入③得

∵  ∴
∴ ∴
∴ ,∵
,∵ ∴
∴ ……………………6分
……………………6分
(Ⅱ) ∵ ,由余弦定理得
,由余弦定理得

 ,--④
,--④
由②得 -⑤ 由④⑤得
-⑤ 由④⑤得 ,∴
,∴ =
= . ……………………………12分
. ……………………………12分
17.解:設(shè)該觀眾先答A題所獲獎(jiǎng)金為 元,先答B(yǎng)題所獲獎(jiǎng)金為
元,先答B(yǎng)題所獲獎(jiǎng)金為 元,………………………1分
元,………………………1分
依題意可得 可能取的值為:0,
可能取的值為:0,  ,3
,3 ,
,  的可能取值為:0,2
的可能取值為:0,2 ,3
,3
………………………2分
∵ ,
, ,
, ,
,
∴ ,
………………………6分
,
………………………6分
∵ ,
, ,
, 
∴ ………………………10分
………………………10分
∵
 ∴
∴ ,即
,即
∴該觀眾應(yīng)先回答B(yǎng)題所獲獎(jiǎng)金的期望較大. ……………………………12分
18.解:(Ⅰ)設(shè) ,由
,由 得
得 ,解得
,解得 或
或 ,若
,若 則
則 與
與 矛盾,所以
矛盾,所以 不合舍去。
不合舍去。
即 。---------------------------------------------------------------------------6
。---------------------------------------------------------------------------6
(Ⅱ)圓 即
即 ,其圓心為C(3,-1),半徑
,其圓心為C(3,-1),半徑 ,
,
∴直線OB的方程為 ,-----------------------------------------------------------------10
,-----------------------------------------------------------------10
設(shè)圓心C(3,-1)關(guān)于直線 的對(duì)稱點(diǎn)的坐標(biāo)為(a,b),則
的對(duì)稱點(diǎn)的坐標(biāo)為(a,b),則

解得: ,則所求的圓的方程為
,則所求的圓的方程為 。-----------------------------14
。-----------------------------14
19.(Ⅰ)證明:∵對(duì)任意的 ①
①
令 得
得 ②…………1分
②…………1分
令 得
得 ……………………2分
……………………2分
∴ 由②得
由②得
∴函數(shù) 為奇函數(shù)………………………………3分
為奇函數(shù)………………………………3分
(Ⅱ)證明:(1)當(dāng)n=1時(shí)等式顯然成立
(2)假設(shè)當(dāng)n=k(k )時(shí)等式成立,即
)時(shí)等式成立,即 ,…………4分
,…………4分
則當(dāng)n=k+1時(shí)有
 ,由①得
,由①得 ………………6分
………………6分
∵ ∴
∴
∴當(dāng)n=k+1時(shí),等式成立。
綜(1)、(2)知對(duì)任意的 ,
, 成立。………………8分
成立。………………8分
(Ⅲ)解:設(shè) ,因函數(shù)
,因函數(shù) 為奇函數(shù),結(jié)合①得
為奇函數(shù),結(jié)合①得
 =
= ,……………………9分
,……………………9分
∵
又∵當(dāng) 時(shí),
時(shí),
∴
 ,∴
,∴
∴函數(shù) 在R上單調(diào)遞減…………………………………………12分
在R上單調(diào)遞減…………………………………………12分
∴

由(2)的結(jié)論得 ,
,
∵ ,∴
,∴ =-2n
=-2n
∵函數(shù) 為奇函數(shù),∴
為奇函數(shù),∴
∴
 ,
, =2n。……………………14分
=2n。……………………14分
20.解:(1)如圖,將側(cè)面BB
 設(shè)棱柱的棱長(zhǎng)為
設(shè)棱柱的棱長(zhǎng)為 ,則B
,則B ,
,
∵CD∥AA1 ∴D為CC1的中點(diǎn),……………………………2分
在Rt△A1AB2中,由勾股定理得 ,
,
即 解得
解得 ,……………………4分
,……………………4分
∵ ∴
∴ ……………………………………6分
……………………………………6分
(2)設(shè)A1B與AB1的交點(diǎn)為O,連結(jié)BB2,OD,則 ……………………………7分
……………………………7分
∵ 平面
平面 ,
, 平面
平面 ∴
∴ 平面
平面 ,
,
即在平面A1BD內(nèi)存在過點(diǎn)D的直線與平面ABC平行 ……………………………9分
(3)連結(jié)AD,B1D ∵ ≌
≌ ≌
≌
∴ ∴
∴ ……………………………11分
……………………………11分
∵ ∴
∴ 平面A1ABB1 ……………………………13分
平面A1ABB1 ……………………………13分
又∵ 平面A1BD ∴平面A1BD⊥平面A1ABB1 ……………………………………14分
平面A1BD ∴平面A1BD⊥平面A1ABB1 ……………………………………14分
21.解:(Ⅰ)
 …………………………………………1分
…………………………………………1分
由 得
得 , ………………………………………………2分
, ………………………………………………2分
又 得
得 ……………………………………………………3分
……………………………………………………3分
(Ⅱ) k=
k=
 ,
,
 對(duì)任意的
對(duì)任意的
 ,即
,即 對(duì)任意的
對(duì)任意的 恒成立……4分
恒成立……4分
等價(jià)于 對(duì)任意的
對(duì)任意的 恒成立。…………………………5分
恒成立。…………………………5分
令g(x)= ,h(x)=
,h(x)= ,
,
則 ,
, …………………………………………6分
…………………………………………6分
 ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng) 時(shí)“=”成立,
時(shí)“=”成立,
 …………7分
…………7分
 h(x)=
h(x)= 在(0,1)上為增函數(shù),
在(0,1)上為增函數(shù), h(x)max<2……………………………8分
h(x)max<2……………………………8分

 ……………………………………………………………………9分
……………………………………………………………………9分
(Ⅲ)設(shè) 則
則 =
= ……10分
……10分
即 ,對(duì)
,對(duì) 恒成立…………………………11分
恒成立…………………………11分

 ,對(duì)
,對(duì) 恒成立
恒成立
即 對(duì)
對(duì) 恒成立…………………………13分
恒成立…………………………13分


解得 ……………………………………………………14分
……………………………………………………14分
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com