
科目: 來源: 題型:
【題目】已知函數f(x)=|x﹣a|+|x+2|.
(1)若a=1.解不等式f(x)≤x2﹣1;
(2)若a>0,b>0,c>0.且f(x)的最小值為4﹣b﹣c.求證:![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】在平面直角坐標系xOy中.直線1的參數方程為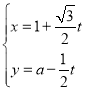 (t為參數).在以坐標原點為極點,x軸的非負半軸為極軸的極坐標系中.曲線C的極坐標方程為ρ=2cosθ.
(t為參數).在以坐標原點為極點,x軸的非負半軸為極軸的極坐標系中.曲線C的極坐標方程為ρ=2cosθ.
(1)若曲線C關于直線l對稱,求a的值;
(2)若A、B為曲線C上兩點.且∠AOB![]() ,求|OA|+|OB|的最大值.
,求|OA|+|OB|的最大值.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖所示的多面體ABCDEF滿足:正方形ABCD與正三角形FBC所在的兩個平面互相垂直,FB∥AE且FB=2EA.
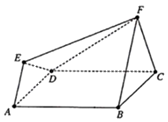
(1)證明:平面EFD⊥平面ABFE;
(2)求二面角E﹣FD﹣C的余弦值.
查看答案和解析>>
科目: 來源: 題型:
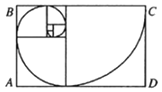
【題目】若數列{an}滿足a1=1,a2=1,an+2=an+an+1,則稱數列{an}為斐波那契數列,斐波那契螺旋線是根據斐波那契數列畫出來的螺旋曲線,自然界中存在許多斐波那契螺旋線的圖案,是自然界最完美的經典黃金比例.作圖規則是在以斐波那契數為邊的正方形拼成的長方形中畫一個圓心角為90°的扇形,連起來的弧線就是斐波那契螺旋線,如圖所示的7個正方形的邊長分別為a1,a2,…,a7,在長方形ABCD內任取一點,則該點不在任何一個扇形內的概率為( )
A.1![]() B.1
B.1![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 來源: 題型:
【題目】2018年非洲豬瘟在東北三省出現,為了進行防控,某地生物醫藥公司派出技術人員對當地甲乙兩個養殖場提供技術服務,方案和收費標準如下:
方案一,公司每天收取養殖場技術服務費40元,對于需要用藥的每頭豬收取藥費2元,不需要用藥的不收費;
方案二,公司每天收取養殖場技術服務費120元,若需要用藥的豬不超過45頭,不另外收費,若需要用藥的豬超過45頭,超過部分每天收取藥費8元.
(1)設日收費為![]() (單位:元),每天需要用藥的豬的數量為
(單位:元),每天需要用藥的豬的數量為![]() ,試寫出兩種方案中
,試寫出兩種方案中![]() 與
與![]() 的函數關系式.
的函數關系式.
(2)若該醫藥公司從10月1日起對甲養殖場提供技術服務,10月31日該養殖場對其中一個豬舍9月份和10月份豬的發病數量進行了統計,得到如下![]() 列聯表.
列聯表.
9月份 | 10月份 | 合計 | |
未發病 | 40 | 85 | 125 |
發病 | 65 | 20 | 85 |
合計 | 105 | 105 | 210 |
根據以上列聯表,判斷是否有![]() 的把握認為豬未發病與醫藥公司提供技術服務有關.
的把握認為豬未發病與醫藥公司提供技術服務有關.
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
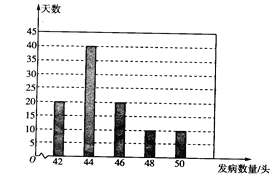
(3)當地的丙養殖場對過去100天豬的發病情況進行了統計,得到如上圖所示的條形統計圖.依據該統計數據,從節約養殖成本的角度去考慮,若丙養殖場計劃結合以往經驗從兩個方案中選擇一個,那么選擇哪個方案更合適,并說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】2018年年底,三部進口影片![]() 登錄銀屏,包括《海王》,《龍貓》和《蜘蛛俠》,經過了解,
登錄銀屏,包括《海王》,《龍貓》和《蜘蛛俠》,經過了解,![]() 電影比《蜘蛛俠》早上映一周,
電影比《蜘蛛俠》早上映一周,![]() 電影的票房比《龍貓》高,《蜘蛛俠》的票房比
電影的票房比《龍貓》高,《蜘蛛俠》的票房比![]() 電影低,據此可以判斷( )
電影低,據此可以判斷( )
A.![]() 是《海王》,
是《海王》,![]() 是《蜘蛛俠》,
是《蜘蛛俠》,![]() 是《龍貓》
是《龍貓》
B.![]() 是《蜘蛛俠》,
是《蜘蛛俠》,![]() 是《龍貓》,
是《龍貓》,![]() 是《海王》
是《海王》
C.![]() 是《龍貓》,
是《龍貓》,![]() 是《海王》,
是《海王》,![]() 是《蜘蛛俠》
是《蜘蛛俠》
D.![]() 是《龍貓》,
是《龍貓》,![]() 是《蜘蛛俠》,
是《蜘蛛俠》,![]() 是《海王》
是《海王》
查看答案和解析>>
科目: 來源: 題型:
【題目】從拋物線![]() 上任意一點
上任意一點![]() 向
向![]() 軸作垂線段垂足為
軸作垂線段垂足為![]() ,點
,點![]() 是線段
是線段![]() 上的一點,且滿足
上的一點,且滿足![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設直線![]() 與軌跡
與軌跡![]() 交于
交于![]() 兩點,點
兩點,點![]() 為軌跡
為軌跡![]() 上異于
上異于![]() 的任意一點,直線
的任意一點,直線![]() 分別與直線
分別與直線![]() 交于
交于![]() 兩點.問:
兩點.問:![]() 軸正半軸上是否存在定點使得以
軸正半軸上是否存在定點使得以![]() 為直徑的圓過該定點?若存在,求出符合條件的定點坐標;若不存在,請說明理由.
為直徑的圓過該定點?若存在,求出符合條件的定點坐標;若不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:
【題目】某互聯網公司為了確定下一季度的前期廣告投入計劃,收集了近![]() 個月廣告投入量
個月廣告投入量![]() (單位:萬元)和收益
(單位:萬元)和收益![]() (單位:萬元)的數據如下表:
(單位:萬元)的數據如下表:
月份 |
|
|
|
|
|
|
廣告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他們分別用兩種模型①![]() ,②
,②![]() 分別進行擬合,得到相應的回歸方程并進行殘差分析,得到如圖所示的殘差圖及一些統計量的值:
分別進行擬合,得到相應的回歸方程并進行殘差分析,得到如圖所示的殘差圖及一些統計量的值:
|
|
|
|
|
|
|
|
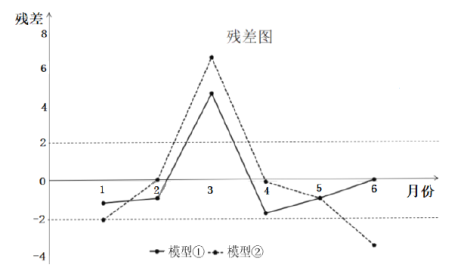
(Ⅰ)根據殘差圖,比較模型①,②的擬合效果,應選擇哪個模型?并說明理由;
(Ⅱ)殘差絕對值大于![]() 的數據被認為是異常數據,需要剔除:
的數據被認為是異常數據,需要剔除:
(ⅰ)剔除異常數據后求出(Ⅰ)中所選模型的回歸方程;
(ⅱ)若廣告投入量![]() 時,該模型收益的預報值是多少?
時,該模型收益的預報值是多少?
附:對于一組數據![]() ,
,![]() ,……,
,……,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為:
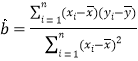
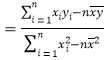 ,
,![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() ),其中離心率
),其中離心率![]() ,點
,點![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() 為橢圓的左右焦點,若
為橢圓的左右焦點,若![]() 面積的最大值為
面積的最大值為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,點
兩點,點![]() 是橢圓
是橢圓![]() 的上頂點,若
的上頂點,若![]() ,試問直線
,試問直線![]() 是否經過定點,若經過定點,求出定點坐標,否則說明理由.
是否經過定點,若經過定點,求出定點坐標,否則說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com