日本成人片在线_久久免费精品视频_国产午夜精品久久久久久免费视_校花撩起jk露出白色内裤国产精品_av影片免费在线观看_国产小视频在线看_最新av免费在线观看_99久久99久久精品国产片_欧美成人猛片aaaaaaa_蜜桃免费网站一区二区三区

【題目】在平面直角坐標系中，當P(x，y)不是原點時，定義P的“伴隨點”為；

當P是原點時，定義P的“伴隨點“為它自身，平面曲線C上所有點的“伴隨點”所構成的曲線定義為曲線C的“伴隨曲線”.現有下列命題：

①若點A的“伴隨點”是點，則點的“伴隨點”是點A

②單位圓的“伴隨曲線”是它自身；

③若曲線C關于x軸對稱，則其“伴隨曲線”關于y軸對稱；

④一條直線的“伴隨曲線”是一條直線.

其中的真命題是_____________（寫出所有真命題的序列）.

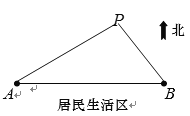
【題目】如圖所示，、是兩個垃圾中轉站，在的正東方向千米處，的南面為居民生活區．為了妥善處理生活垃圾，政府決定在的北面建一個垃圾發電廠．垃圾發電廠的選址擬滿足以下兩個要求（、、可看成三個點）：①垃圾發電廠到兩個垃圾中轉站的距離與它們每天集中的生活垃圾量成反比，比例系數相同；②垃圾發電廠應盡量遠離居民區（這里參考的指標是點到直線的距離要盡可能大）．現估測得、兩個中轉站每天集中的生活垃圾量分別約為噸和噸．設．

（1）求（用的表達式表示）；

（2）垃圾發電廠該如何選址才能同時滿足上述要求？

【題目】已知正項數列，滿足：對任意正整數，都有，，成等差數列，，，成等比數列，且，．

（Ⅰ）求證：數列是等差數列；

（Ⅱ）求數列，的通項公式；

（Ⅲ）設=++…+，如果對任意的正整數，不等式恒成立，求實數的取值范圍．

【題目】定義在上的函數，如果滿足：對任意，存在常數，都有成立，則稱是上的有界函數，其中稱為函數的上界．

（1）設，判斷在上是否為有界函數，若是，請說明理由，并寫出的所有上界的集合；若不是，也請說明理由；

（2）若函數在上是以為上界的有界函數，求實數的取值范圍．

【題目】已知正項數列，滿足：對任意正整數，都有，，成等差數列，，，成等比數列，且，．

（Ⅰ）求證：數列是等差數列；

（Ⅱ）求數列，的通項公式；

（Ⅲ）設=++…+，如果對任意的正整數，不等式恒成立，求實數的取值范圍．

【題目】定義上的函數,若滿足:對任意,存在常數,都有成立,則稱是上的有界函數,其中稱為函數的上界.

(1)設,判斷在上是否有界函數,若是,請說明理由,并寫出的所有上界的值的集合,若不是,也請說明理由;

(2)若函數在上是以3為上界的有界函數,求實數的取值范圍.

【題目】已知數列、滿足：，，，．

（1）求，，，；

（2）求證：數列是等差數列，并求的通項公式；

（3）設，若不等式對任意恒成立，求實數的取值范圍．

【題目】設橢圓：（）的右焦點為，短軸的一個端點到的距離等于焦距．

（1）求橢圓的標準方程；

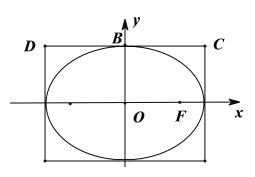
（2）設、是四條直線，所圍成的矩形在第一、第二象限的兩個頂點，是橢圓上任意一點，若，求證：為定值；

（3）過點的直線與橢圓交于不同的兩點、，且滿足△與△的面積的比值為，求直線的方程．

【題目】定義在上的函數，如果滿足：對任意，存在常數，都有成立，則稱是上的有界函數，其中稱為函數的上界．

（1）設，判斷在上是否為有界函數，若是，請說明理由，并寫出的所有上界的集合；若不是，也請說明理由；

（2）若函數在上是以為上界的有界函數，求實數的取值范圍．