
【題目】定義在![]() 上的函數
上的函數![]() ,如果滿足:對任意
,如果滿足:對任意![]() ,存在常數
,存在常數![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 是
是![]() 上的有界函數,其中
上的有界函數,其中![]() 稱為函數
稱為函數![]() 的上界.
的上界.
(1)設![]() ,判斷
,判斷![]() 在
在![]() 上是否為有界函數,若是,請說明理由,并寫出
上是否為有界函數,若是,請說明理由,并寫出![]() 的所有上界
的所有上界![]() 的集合;若不是,也請說明理由;
的集合;若不是,也請說明理由;
(2)若函數![]() 在
在![]() 上是以
上是以![]() 為上界的有界函數,求實數
為上界的有界函數,求實數![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】設數列![]() 的所有項都是不等于
的所有項都是不等于![]() 的正數,
的正數,![]() 的前
的前![]() 項和為
項和為![]() ,已知點
,已知點![]() 在直線
在直線![]() 上(其中常數
上(其中常數![]() ,且
,且![]() )數列,又
)數列,又![]() .
.
(1)求證數列![]() 是等比數列;
是等比數列;
(2)如果![]() ,求實數
,求實數![]() 的值;
的值;
(3)若果存在![]() 使得點
使得點![]() 和
和![]() 都在直線在
都在直線在![]() 上,是否存在自然數
上,是否存在自然數![]() ,當
,當![]() (
(![]() )時,
)時,![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最小值;若不存在,請說明理由.
的最小值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記點![]() 到圖形
到圖形![]() 上每一個點的距離的最小值稱為點
上每一個點的距離的最小值稱為點![]() 到圖形
到圖形![]() 的距離,那么平面內到定圓
的距離,那么平面內到定圓![]() 的距離與到定點
的距離與到定點![]() 的距離相等的點的軌跡不可能是 ( )
的距離相等的點的軌跡不可能是 ( )
A.圓B.橢圓C.雙曲線的一支D.直線
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于數列![]() ,稱
,稱![]() (其中
(其中![]() )為數列
)為數列![]() 的前k項“波動均值”.若對任意的
的前k項“波動均值”.若對任意的![]() ,都有
,都有![]() ,則稱數列
,則稱數列![]() 為“趨穩數列”.
為“趨穩數列”.
(1)若數列1,![]() ,2為“趨穩數列”,求
,2為“趨穩數列”,求![]() 的取值范圍;
的取值范圍;
(2)若各項均為正數的等比數列![]() 的公比
的公比![]() ,求證:
,求證:![]() 是“趨穩數列”;
是“趨穩數列”;
(3)已知數列![]() 的首項為1,各項均為整數,前
的首項為1,各項均為整數,前![]() 項的和為
項的和為![]() . 且對任意
. 且對任意![]() ,都有
,都有![]() , 試計算:
, 試計算:![]() (
(![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 為函數
為函數![]() (
(![]() ,
,![]() 為定義域)圖像上的一個動點,
為定義域)圖像上的一個動點,![]() 為坐標原點,
為坐標原點,![]() 為點
為點![]() 與點
與點![]() 兩點間的距離.
兩點間的距離.
(1)若![]() ,求
,求![]() 的最大值與最小值;
的最大值與最小值;
(2)若![]() ,是否存在實數
,是否存在實數![]() ,使得
,使得![]() 的最小值不小于2?若存在,請求出
的最小值不小于2?若存在,請求出![]() 的取值范圍;若不存在,則說明理由.
的取值范圍;若不存在,則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年反映社會現實的電影《我不是藥神》引起了很大的轟動,治療特種病的創新藥研發成了當務之急.為此,某藥企加大了研發投入,市場上治療一類慢性病的特效藥品![]() 的研發費用
的研發費用![]() (百萬元)和銷量
(百萬元)和銷量![]() (萬盒)的統計數據如下:
(萬盒)的統計數據如下:
研發費用 | 2 | 3 | 6 | 10 | 13 | 15 | 18 | 21 |
銷量 | 1 | 1 | 2 | 2.5 | 3.5 | 3.5 | 4.5 | 6 |
(1)求![]() 與
與![]() 的相關系數
的相關系數![]() 精確到0.01,并判斷
精確到0.01,并判斷![]() 與
與![]() 的關系是否可用線性回歸方程模型擬合?(規定:
的關系是否可用線性回歸方程模型擬合?(規定:![]() 時,可用線性回歸方程模型擬合);
時,可用線性回歸方程模型擬合);
(2)該藥企準備生產藥品![]() 的三類不同的劑型
的三類不同的劑型![]() ,
,![]() ,
,![]() ,并對其進行兩次檢測,當第一次檢測合格后,才能進行第二次檢測.第一次檢測時,三類劑型
,并對其進行兩次檢測,當第一次檢測合格后,才能進行第二次檢測.第一次檢測時,三類劑型![]() ,
,![]() ,
,![]() 合格的概率分別為
合格的概率分別為![]() ,
,![]() ,
,![]() ,第二次檢測時,三類劑型
,第二次檢測時,三類劑型![]() ,
,![]() ,
,![]() 合格的概率分別為
合格的概率分別為![]() ,
,![]() ,
,![]() .兩次檢測過程相互獨立,設經過兩次檢測后
.兩次檢測過程相互獨立,設經過兩次檢測后![]() ,
,![]() ,
,![]() 三類劑型合格的種類數為
三類劑型合格的種類數為![]() ,求
,求![]() 的數學期望.
的數學期望.
附:(1)相關系數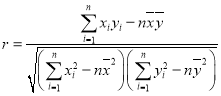
(2)![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為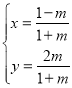 (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)過點![]() 作傾斜角為
作傾斜角為![]() 的直線
的直線![]() 交
交![]() 于
于![]() 兩點,過
兩點,過![]() 作與
作與![]() 平行的直線
平行的直線![]() 交
交![]() 于
于![]() 點,若
點,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是定義在
是定義在![]() 上的函數,如果存在常數
上的函數,如果存在常數![]() ,對區間
,對區間![]() 的任意劃分:
的任意劃分:![]() ,和式
,和式![]() 恒成立,則稱
恒成立,則稱![]() 為
為![]() 上的“絕對差有界函數”。注:
上的“絕對差有界函數”。注:![]() 。
。
(1)證明函數![]() 在
在![]() 上是“絕對差有界函數”。
上是“絕對差有界函數”。
(2)證明函數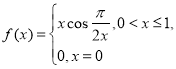 不是
不是![]() 上的“絕對差有界函數”。
上的“絕對差有界函數”。
(3)記集合![]() 存在常數
存在常數![]() ,對任意的
,對任意的![]() ,有
,有![]() 成立
成立![]() ,證明集合
,證明集合![]() 中的任意函數
中的任意函數![]() 為“絕對差有界函數”,并判斷
為“絕對差有界函數”,并判斷![]() 是否在集合
是否在集合![]() 中,如果在,請證明并求
中,如果在,請證明并求![]() 的最小值;如果不在,請說明理由。
的最小值;如果不在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某甲![]() 籃球隊的12名隊員(含2名外援)中有5名主力隊員(含一名外援),主教練要從12名隊員中選5人首發上場,則主力隊員不少于4人,且有一名外援上場的概率是_____.
籃球隊的12名隊員(含2名外援)中有5名主力隊員(含一名外援),主教練要從12名隊員中選5人首發上場,則主力隊員不少于4人,且有一名外援上場的概率是_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com