日本成人片在线_久久免费精品视频_国产午夜精品久久久久久免费视_校花撩起jk露出白色内裤国产精品_av影片免费在线观看_国产小视频在线看_最新av免费在线观看_99久久99久久精品国产片_欧美成人猛片aaaaaaa_蜜桃免费网站一区二区三区

【題目】已知等比數(shù)列的首項，數(shù)列前項和記為，前項積記為.

(1) 若，求等比數(shù)列的公比；

(2) 在(1)的條件下，判斷與的大小；并求為何值時，取得最大值；

(3) 在(1)的條件下，證明：若數(shù)列中的任意相鄰三項按從小到大排列，則總可以使其成等差數(shù)列；若所有這些等差數(shù)列的公差按從小到大的順序依次記為，則數(shù)列為等比數(shù)列.

【題目】對于函數(shù)，若在定義域內(nèi)存在實數(shù)，滿足，則稱為“局部奇函數(shù)”.

(1)已知二次函數(shù)，試判斷是否為“局部奇函數(shù)”？并說明理由；

(2)若是定義在區(qū)間上的“局部奇函數(shù)”，求實數(shù)的取值范圍；

(3)若為定義域上的“局部奇函數(shù)”，求實數(shù)的取值范圍；

【題目】已知橢圓的右頂點、上頂點分別為A、B，坐標原點到直線AB的距離為，且.

（1）求橢圓C的方程；

（2）過橢圓C的左焦點的直線交橢圓于M、N兩點，且該橢圓上存在點P，使得四邊形MONP（圖形上字母按此順序排列）恰好為平行四邊形，求直線的方程.

【題目】已知函數(shù)f(x),g(x)=|xlnx﹣ax2|,a.

(1)討論f(x)的單調(diào)性;

(2)若g(x)在區(qū)間(1,e)有極小值,求a的取值范圍.

(Ⅰ)求C的方程;

(Ⅱ)斜率為﹣1的直線與C交于異于點P的兩個不同的點M,N,若直線PM,PN分別與x軸交于A,B兩點,求證:△PAB為等腰三角形.

【題目】某中學(xué)的甲、乙、丙三名同學(xué)參加高校自主招生考試，每位同學(xué)彼此獨立的從四所高校中選2所.

（Ⅰ）求甲、乙、丙三名同學(xué)都選高校的概率；

（Ⅱ）若已知甲同學(xué)特別喜歡高校，他必選校，另在三校中再隨機選1所；而同學(xué)乙和丙對四所高校沒有偏愛，因此他們每人在四所高校中隨機選2所.

（ⅰ）求甲同學(xué)選高校且乙、丙都未選高校的概率；

（ⅱ）記為甲、乙、丙三名同學(xué)中選校的人數(shù)，求隨機變量的分布列及數(shù)學(xué)期望.

【題目】如圖,在六棱錐P﹣ABCDEF中,六邊形ABCDEF為正六邊形,平面PAB⊥平面ABCDEF,AB=1,PA,PB=2.

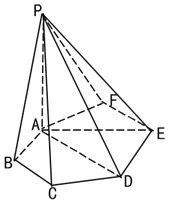
(1)求證:PA⊥平面ABCDEF;

(2)求直線PD與平面PAE所成角的正弦值.

(Ⅰ)求數(shù)列{an}與{bn}的通項公式;

(Ⅱ)設(shè)數(shù)列{cn}滿足cn=an+bn,求數(shù)列{cn}的前n項和Tn.

【題目】已知函數(shù)f(x)=()|x|,若函數(shù)g(x)=f(x﹣1)+a(ex﹣1+e﹣x+1)存在最大值M,則實數(shù)a的取值范圍為_____

【題目】已知項數(shù)為的數(shù)列滿足如下條件:①；②.若數(shù)列滿足,其中,則稱為的“伴隨數(shù)列”.

(1)數(shù)列1,3,5,7,9是否存在“伴隨數(shù)列”,若存在,寫出其“伴隨數(shù)列”；若不存在,請說明理由；

(2)若為的“伴隨數(shù)列”,證明:；

(3)已知數(shù)列存在“伴隨數(shù)列”,且,,求m的最大值.