
科目: 來源: 題型:解答題
函數f(x)=6cos2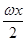 +
+ sin ωx-3(ω>0)在一個周期內的圖象如圖所示,A為圖象的最高點,B,C為圖象與x軸的交點,且△ABC為正三角形.
sin ωx-3(ω>0)在一個周期內的圖象如圖所示,A為圖象的最高點,B,C為圖象與x軸的交點,且△ABC為正三角形.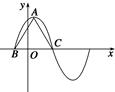
(1)求ω的值及函數f(x)的值域;
(2)若f(x0)=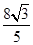 ,且x0∈
,且x0∈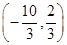 ,求f(x0+1)的值.
,求f(x0+1)的值.
查看答案和解析>>
科目: 來源: 題型:解答題
已知向量m=(sin x,1),n= ,函數f(x)=(m+n)·m.
,函數f(x)=(m+n)·m.
(1)求函數f(x)的最小正周期T及單調遞增區間;
(2)已知a,b,c分別為△ABC內角A,B,C的對邊,A為銳角,a=2 ,c=4,且f(A)是函數f(x)在
,c=4,且f(A)是函數f(x)在 上的最大值,求△ABC的面積S.
上的最大值,求△ABC的面積S.
查看答案和解析>>
科目: 來源: 題型:解答題
(2013·佛山模擬)在平面直角坐標系xOy中,以Ox為始邊,角α的終邊與單位圓O的交點B在第一象限,已知A(-1,3).
(1)若OA⊥OB,求tan α的值;
(2)若B點橫坐標為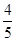 ,求S△AOB.
,求S△AOB.
查看答案和解析>>
科目: 來源: 題型:解答題
已知向量a=(cosωx,sinωx),b=(cosωx,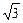 cosωx),其中0<ω<2,函數
cosωx),其中0<ω<2,函數 ,其圖象的一條對稱軸為
,其圖象的一條對稱軸為 。
。
(1)求函數的表達式及單調遞增區間;
(2)在△ABC中,a,b,c分別是角A,B,C的對邊,S△ABC為其面積,若 ,b=1,
,b=1,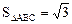 ,求a的值。
,求a的值。
查看答案和解析>>
科目: 來源: 題型:解答題
設向量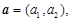
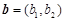 ,定義一種向量積
,定義一種向量積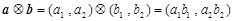 .
.
已知向量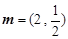 ,
,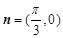 ,點
,點 為
為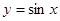 的圖象上的動點,點
的圖象上的動點,點
為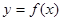 的圖象上的動點,且滿足
的圖象上的動點,且滿足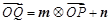 (其中
(其中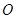 為坐標原點).
為坐標原點).
(1)請用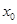 表示
表示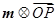 ;
;
(2)求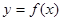 的表達式并求它的周期;
的表達式并求它的周期;
(3)把函數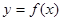 圖象上各點的橫坐標縮小為原來的
圖象上各點的橫坐標縮小為原來的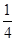 倍(縱坐標不變),得到函數
倍(縱坐標不變),得到函數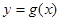 的圖象.設函數
的圖象.設函數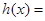
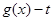
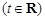 ,試討論函數
,試討論函數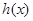 在區間
在區間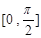 內的零點個數.
內的零點個數.
查看答案和解析>>
科目: 來源: 題型:解答題
若函數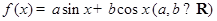 ,非零向量
,非零向量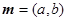 ,我們稱
,我們稱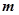 為函數
為函數 的“相伴向量”,
的“相伴向量”, 為向量
為向量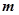 的“相伴函數”.
的“相伴函數”.
(1)已知函數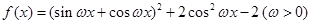 的最小正周期為
的最小正周期為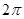 ,求函數
,求函數 的“相伴向量”;
的“相伴向量”;
(2)記向量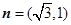 的“相伴函數”為
的“相伴函數”為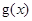 ,將
,將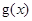 圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再將所得的圖象上所有點向左平移
圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再將所得的圖象上所有點向左平移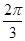 個單位長度,得到函數
個單位長度,得到函數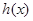 ,若
,若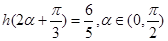 ,求
,求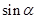 的值;
的值;
(3)對于函數 ,是否存在“相伴向量”?若存在,求出
,是否存在“相伴向量”?若存在,求出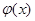 “相伴向量”;
“相伴向量”;
若不存在,請說明理由.
查看答案和解析>>
科目: 來源: 題型:解答題
已知函數y=3sin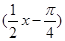
(1)用五點法在給定的坐標系中作出函數一個周期的圖象;
(2)求此函數的振幅、周期和初相;
(3)求此函數圖象的對稱軸方程、對稱中心.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com