
某公路段在某一時刻內監測到的車速頻率分布直方圖如圖所示.
(Ⅰ)求縱坐標中參數h的值及第三個小長方形的面積;
(Ⅱ)求車速的眾數v1,中位數v2的估計值;
(Ⅲ)求平均車速 的估計值.
的估計值.
(Ⅰ)0.4;(Ⅱ)62.5;(Ⅲ)62.
解析試題分析:(Ⅰ)所有小長形面積之和為1,由此求出h=0.01,從而能求出第三個小長方形的面積.(Ⅱ)利用頻率分布直方圖估計車速的眾數就是最高矩形方框中點的橫坐標,而車速的中位數就是在中位數兩邊直方圖的面積相等.(Ⅲ)利用頻率分布直方圖及估值公式: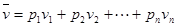 (其中
(其中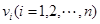 是各直方圖的中點的橫坐標,
是各直方圖的中點的橫坐標,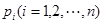 是各直方圖的面積)能求出平均車速
是各直方圖的面積)能求出平均車速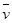 .
.
試題解析:(Ⅰ)∵所有小長形面積之和為1,
∴10h+10×3h+10×4h+10×2h=1,
解得h=0.01,
∴第三個小長方形的面積為:10×4h=10×0.04=0.4.
(Ⅱ)車速的眾數v1=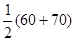 =65,
=65,
車速的中位數是兩邊直方圖的面積相等,
于是得:10×0.01+10×0.03+(v2﹣60)×0.04=0.5,
解得v2=62.5.
(Ⅲ)平均車速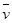 =0.01×10×45+0.03×10×55+0.04×10×65+0.02×10×75=62.
=0.01×10×45+0.03×10×55+0.04×10×65+0.02×10×75=62.
考點:頻率分布直方圖的應用.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
某班主任對班級22名學生進行了作業量多少的調查,數據如下表:在喜歡玩電腦游戲的12中,有10人認為作業多,2人認為作業不多;在不喜歡玩電腦游戲的10人中,有3人認為作業多,7人認為作業不多。求:(1)根據以上數據建立一個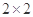 列聯表;(2)試問喜歡電腦游戲與認為作業多少是否有關系?
列聯表;(2)試問喜歡電腦游戲與認為作業多少是否有關系?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
廠家在產品出廠前,需對產品做檢驗,廠家將一批產品發給商家時,商家按合同規定也需隨機抽取一定數量的產品做檢驗,以決定是否接收這批產品.
(1)若廠家庫房中的每件產品合格的概率為0.8,從中任意取出4件進行檢驗,求至少有1件是合格品的概率;
(2)若廠家發給商家20件產品,其中有3件不合格.按合同規定該商家從中任取2件進行檢驗,只有2件都合格時才接收這批產品,否則拒收.求該商家可能檢驗出不合格產品數ξ的分布列及數學期望E(ξ),并求該商家拒收這批產品的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某高校共有15000人,其中男生10500人,女生4500人,為調查該校學生每周平均體育運動時間的情況,采用分層抽樣的方法,收集300位學生每周平均體育運動時間的樣本數據(單位:小時)
(1)應收集多少位女生樣本數據?
(2)根據這300個樣本數據,得到學生每周平均體育運動時間的頻率分布直方圖(如圖所示),其中樣本數據分組區間為: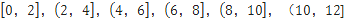 .估計該校學生每周平均體育運動時間超過4個小時的概率.
.估計該校學生每周平均體育運動時間超過4個小時的概率.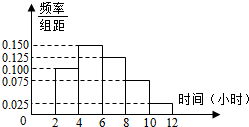
(3)在樣本數據中,有60位女生的每周平均體育運動時間超過4個小時.請完成每周平均體育運動時間與性別的列聯表,并判斷是否有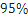 的把握認為“該校學生的每周平均體育運動時間與性別有關”.
的把握認為“該校學生的每周平均體育運動時間與性別有關”.
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
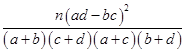
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了解某班學生喜愛打籃球是否與性別有關,對本班50人進行了問卷調查得到了如下的列聯表:
| | 喜愛打籃球 | 不喜愛打籃球 | 合計 |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合計 | 30 | 20 | 50 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某化肥廠甲、乙兩個車間包裝肥料,在自動包裝傳送帶上每隔30 min抽取一包產品,稱其重量,分別記錄抽查數據如下:
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)這種抽樣方法是哪一種?
(2)將這兩組數據用莖葉圖表示;
(3)將兩組數據比較,說明哪個車間的產品較穩定.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
某市高三數學抽樣考試中,對90分以上
(含90分)的成績進行統計,其頻率分布圖
如圖所示,若130—140分數段的人數為90人,
則90—100分數段的人數為_______
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com