
【題目】已知函數h(x)=ax3﹣1(a∈R),g(x)=lnx,f(x)=h(x)+3xg(x)(e為自然對數的底數).
(I)若f(x)圖象過點(1,﹣1),求f(x)的單調區間;
(II)若f(x)在區間( ![]() ,e)上有且只有一個極值點,求實數a的取值范圍;
,e)上有且只有一個極值點,求實數a的取值范圍;
(III)函數F(x)=(a﹣ ![]() )x3+
)x3+ ![]() x2g(a)﹣h(x)﹣1,當a>e
x2g(a)﹣h(x)﹣1,當a>e ![]() 時,函數F(x)過點A(1,m)的切線至少有2條,求實數m的值.
時,函數F(x)過點A(1,m)的切線至少有2條,求實數m的值.
【答案】解:(Ⅰ)由已知f(x)=h(x)+3xg(x)=ax3﹣1+3xlnx,
又f(x)過點(1,﹣1),所以a=0,
∴f(x)=3xlnx﹣1,且定義域為(0,+∞),
f′(x)=3lnx+3=3(lnx+1),
令f′(x)>0,解得:x> ![]() ,令f′(x)<0,解得:0<x<
,令f′(x)<0,解得:0<x< ![]() ,
,
故f(x)=3xlnx﹣1在(0, ![]() )上是減函數,在(
)上是減函數,在( ![]() ,+∞)上是增函數;
,+∞)上是增函數;
(Ⅱ)函數f(x)=ax3+3xlnx﹣1的定義域為(0,+∞),
f′(x)=3(ax2+lnx+1),
令r(x)=ax2+lnx+1,
則r′(x)=2ax+ ![]() =
= ![]() ,
,
當a>0時,r′(x)>0在(0,+∞)恒成立,
故f′(x)=3(ax2+lnx+1)在(0,+∞)上是增函數,
而f′( ![]() )=
)= ![]() >0,
>0,
故當x∈( ![]() ,e)時,f′(x)>0恒成立,
,e)時,f′(x)>0恒成立,
故f(x)在區間( ![]() ,e)上單調遞增,
,e)上單調遞增,
故f(x)在區間( ![]() ,e)上沒有極值點;
,e)上沒有極值點;
當a=0時,由(Ⅰ)知,f(x)在區間( ![]() ,e)上沒有極值點;
,e)上沒有極值點;
當a<0時,令 ![]() =0,解得,x=
=0,解得,x= ![]() ;
;
故r(x)=ax2+lnx+1在(0, ![]() )上是增函數,在(
)上是增函數,在( ![]() ,+∞)上是減函數,
,+∞)上是減函數,
①當r(e)r( ![]() )<0,即﹣
)<0,即﹣ ![]() <a<0時,
<a<0時,
r(x)在( ![]() ,e)上有且只有一個零點,且在該零點兩側異號,
,e)上有且只有一個零點,且在該零點兩側異號,
②令r( ![]() )=0,得
)=0,得 ![]() =0,不成立;
=0,不成立;
③令r(e)=0,得a=﹣ ![]() ,所以
,所以 ![]() ∈(
∈( ![]() ,e),
,e),
而r( ![]() )=r(
)=r( ![]() )=
)= ![]() +ln
+ln ![]() >0,又r(
>0,又r( ![]() )<0,
)<0,
所以r(x)在( ![]() ,e)上有且只有一個零點,且在該零點兩側異號,
,e)上有且只有一個零點,且在該零點兩側異號,
綜上所述,實數a的取值范圍是[﹣ ![]() ,0).
,0).
(Ⅲ)函數F(x)=(a﹣ ![]() )x3+
)x3+ ![]() x2g(a)﹣h(x)﹣1,
x2g(a)﹣h(x)﹣1,
由函數F(x)過點A(1,m)的切線,
所以m= ![]() x03﹣(1+
x03﹣(1+ ![]() lna)x02+x0lna,(*)
lna)x02+x0lna,(*)
②據題意,原命題等價于關于x0的方程(*)至少有2個不同的解.
設φ(x)= ![]() x3﹣(1+
x3﹣(1+ ![]() lna)x2+xlna,
lna)x2+xlna,
φ′(x)=2x2﹣(2+lna)x+lna=(x﹣1)(2x﹣lna),
因為a> ![]() ,所以
,所以 ![]() lna>
lna> ![]() >1,
>1,
當x∈(﹣∞,1)和( ![]() lna,+∞)時,φ′(x)>0,φ(x)為增函數;
lna,+∞)時,φ′(x)>0,φ(x)為增函數;
當x∈(1, ![]() lna)時,φ′(x)<0,φ(x)為減函數;
lna)時,φ′(x)<0,φ(x)為減函數;
所以φ(x)的極大值為φ(1)= ![]() lna﹣
lna﹣ ![]() ,
,
φ(x)的極小值為φ( ![]() lna)=﹣
lna)=﹣ ![]() ln3a+
ln3a+ ![]() ln2a,
ln2a,
設lna=t,t> ![]() ,
,
則原命題等價于 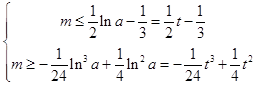 對t>
對t> ![]() 恒成立,
恒成立,
所以由m≤ ![]() t﹣
t﹣ ![]() 對t>
對t> ![]() 恒成立,得m≤
恒成立,得m≤ ![]() ; (1)
; (1)
記s(t)=﹣ ![]() t3+
t3+ ![]() t2 , s′(t)=﹣
t2 , s′(t)=﹣ ![]() t2+
t2+ ![]() t=
t= ![]() t(1﹣
t(1﹣ ![]() t),
t),
所以t> ![]() 時,s(t)的最大值為s(4)=
時,s(t)的最大值為s(4)= ![]() ,由m≥﹣
,由m≥﹣ ![]() t3+
t3+ ![]() t2對t>
t2對t> ![]() 恒成立,得m≥
恒成立,得m≥ ![]() . (2)
. (2)
由(1)(2)得,m= ![]() .
.
綜上,當a> ![]() ,實數m的值為
,實數m的值為 ![]() 時,函數F(x)過點A(1,m)的切線至少有2條
時,函數F(x)過點A(1,m)的切線至少有2條
【解析】(Ⅰ)求出f(x)的導數,解關于導函數的不等式,求出函數的單調區間即可;(Ⅱ)求出f(x)的導數,通過討論a的范圍求出函數的單調區間,結合已知條件求出a的范圍即可;(Ⅲ)求出函數的導數,求出B處的切線方程,根據函數的單調性求出a的范圍即可.
【考點精析】認真審題,首先需要了解利用導數研究函數的單調性(一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減),還要掌握函數的極值與導數(求函數
在這個區間單調遞減),還要掌握函數的極值與導數(求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值)的相關知識才是答題的關鍵.
是極小值)的相關知識才是答題的關鍵.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(2sin
=(2sin ![]() ,2sin
,2sin ![]() ),
), ![]() =(cos
=(cos ![]() ,﹣
,﹣ ![]() sin
sin ![]() ). (Ⅰ)求函數f(x)=
). (Ⅰ)求函數f(x)= ![]()
![]() +
+ ![]() 的最小正周期;
的最小正周期;
(Ⅱ)若β= ![]() ,g(β)=tan2α,α≠
,g(β)=tan2α,α≠ ![]() +
+ ![]() 且α≠
且α≠ ![]() +kπ(k∈Z),數列{an}滿足a1=
+kπ(k∈Z),數列{an}滿足a1= ![]() ,an+12=
,an+12= ![]() ang(an)(n≤16且n∈N*),令bn=
ang(an)(n≤16且n∈N*),令bn= ![]() ,求數列{bn}的通項公式及前n項和Sn .
,求數列{bn}的通項公式及前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三共有900名學生,高三模擬考之后,為了了解學生學習情況,用分層抽樣方法從中抽出若干學生此次數學成績,按成績分組,制成如下的頻率分布表:
組號 | 第一組 | 第二組 | 第二組 | 第四組 |
分組 | [70,80) | [80,90) | [90,100) | [100,110) |
頻數 | 6 | 4 | 22 | 20 |
頻率 | 0.06 | 0.04 | 0.22 | 0.20 |
組號 | 第五組 | 第六組 | 第七組 | 第八組 |
分組 | [110,120) | [120,130) | [130,140) | [140,150] |
頻數 | 18 | a | 10 | 5 |
頻率 | b | 0.15 | 0.10 | 0.05 |
(1)若頻數的總和為c,試求a,b,c的值;
(2)為了了解數學成績在120分以上的學生的心理狀態,現決定在第六、七、八組中用分層抽樣方法抽取6名學生,在這6名學生中又再隨機抽取2名與心理老師面談,令第七組被抽中的學生數為隨機變量ξ,求隨機變量ξ的分布列和數學期望;
(3)估計該校本次考試的數學平均分.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() (其中e是自然對數的底數,a∈R). (Ⅰ)若曲線f(x)在x=l處的切線與x軸不平行,求a的值;
(其中e是自然對數的底數,a∈R). (Ⅰ)若曲線f(x)在x=l處的切線與x軸不平行,求a的值;
(Ⅱ)若函數f(x)在區間(0,1]上是單調函數,求a的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:函數y=log0.5(x2+2x+a)的值域R,命題q:函數y=x2a﹣5在(0,+∞)上是減函數.若p或q為真命題,p且q為假命題,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)在R上可導,其導函數為f′(x),且函數y=(1﹣x)f′(x)的圖象如圖所示,則下列結論中一定成立的是( ) 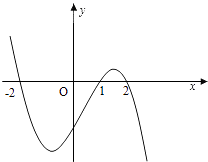
A.函數f(x)有極大值f(2)和極小值f(1)
B.函數f(x)有極大值f(﹣2)和極小值f(1)
C.函數f(x)有極大值f(2)和極小值f(﹣2)
D.函數f(x)有極大值f(﹣2)和極小值f(2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了得到 ![]() 函數的圖象,只需把y=3sinx上所有的點( )
函數的圖象,只需把y=3sinx上所有的點( )
A.先把橫坐標縮短到原來的 ![]() 倍,然后向左平移
倍,然后向左平移 ![]() 個單位
個單位
B.先把橫坐標縮短到原來的2倍,然后向左平移 ![]() 個單位
個單位
C.先把橫坐標縮短到原來的2倍,然后向左右移 ![]() 個單位
個單位
D.先把橫坐標縮短到原來的 ![]() 倍,然后向右平移
倍,然后向右平移 ![]() 個單位
個單位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以直角坐標系的原點O為極點,x軸的正半軸為極軸,且兩個坐標系取相同的單位長度,已知直線I的參數方程為 ![]() (t為參數),圓C的極坐標方程為ρ=2,點P關于極點對稱的點P'QUOTE p的極坐標為
(t為參數),圓C的極坐標方程為ρ=2,點P關于極點對稱的點P'QUOTE p的極坐標為 ![]()
(1)寫出圓C的直角坐標方程及點P的極坐標;
(2)設直線I與圓C相交于兩點A、B,求點P到A、B兩點的距離之積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】血藥濃度(Plasma Concentration)是指藥物吸收后在血漿內的總濃度.藥物在人體內發揮治療作用時,該藥物的血藥濃度應介于最低有效濃度和最低中毒濃度之間.已知成人單次服用1單位某藥物后,體內血藥濃度及相關信息如圖所示: 
根據圖中提供的信息,下列關于成人使用該藥物的說法中,不正確的個數是( )
①首次服用該藥物1單位約10分鐘后,藥物發揮治療作用
②每次服用該藥物1單位,兩次服藥間隔小于2小時,一定會產生藥物中毒
③每間隔5.5小時服用該藥物1單位,可使藥物持續發揮治療作用
④首次服用該藥物1單位3小時后,再次服用該藥物1單位,不會發生藥物中毒.
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com