【題目】某校學生會為了解高二年級600名學生課余時間參加中華傳統文化活動的情況(每名學生最多參加7場).隨機抽取50名學生進行調查，將數據分組整理后，列表如下:
則以下四個結論中正確的是( )
A.表中
的數值為10
B.估計該年級參加中華傳統文化活動場數不高于2場的學生約為108人
C.估計該年級參加中華傳統文化活動場數不低于4場的學生約為216人
D.若采用系統抽樣方法進行調查，從該校高二600名學生中抽取容量為30的樣本，則分段間隔為15
陽光試卷單元測試卷系列答案科目：高中數學 來源： 題型：
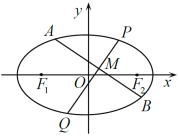
【題目】如圖，
、
是離心率為
的橢圓
：
的左、右焦點，過作
軸的垂線交橢圓所得弦長為
，設
、
是橢圓上的兩個動點，線段
的中垂線與橢圓交于
、
兩點，線段的中點
的橫坐標為1.
（1）求橢圓的方程；
（2）求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了引導居民合理用電，國家決定實行合理的階梯電價，居民用電原則上以住宅為單位（一套住宅為一戶）.
階梯級別 | 第一階梯 | 第二階梯 | 第三階梯 |
月用電范圍（度） | （0,210] | （210,400] |
|
某市隨機抽取10戶同一個月的用電情況，得到統計表如下：
居民用電戶編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用電量（度） | 53 | 86 | 90 | 124 | 132 | 200 | 215 | 225 | 300 | 410 |
若規定第一階梯電價每度0.5元，第二階梯超出第一階梯的部分每度0.6元，第三階梯超出第二階梯的部分每度0.8元，試計算A居民用電戶用電410度時應電費多少元？
現要在這10戶家庭中任意選取3戶，求取到第二階梯電量的戶數的分布列與期望；
以表中抽到的10戶作為樣本估計全市的居民用電，現從全市中依次抽取10戶，若抽到
戶用電量為第一階梯的可能性最大，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著我國經濟的高速發展，汽車的銷量也快速增加，每年因道路交通安全事故造成傷亡人數超過
萬人，根據國家質量監督檢驗檢疫局發布的《車輛駕駛人員血液、呼氣酒精含量閥值與檢驗》（
-醉駕車的測試
）的規定：飲酒駕車是指車輛駕駛人員血液中的酒精含量大于或者等于
，小于
的駕駛行為；醉酒駕車是指車輛駕駛人員血液中的酒精含量大于或者等于的駕駛行為，某市交通部門從
年飲酒后駕駛機動車輛發生交通事故的駕駛員中隨機抽查了
人進行統計，得到如下數據：
酒精含量
|
|
|
|
|
|
發生交通事故的人數 |
|
|
|
|
|
已知從這人中任意抽取兩人，兩人均是醉酒駕車的概率是
.
（1）求
，
的值；
（2）實踐證明，駕駛人員血液中的酒精含量與發生交通事故的人數具有線性相關性，試建立
關于
的線性回歸方程；
（3）試預測，駕駛人員血液中的酒精含量為多少時，發生交通事故的人數會超過取樣人數的
？
參考數據：
，
回歸直線方程
中系數計算公式
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為培養學生的閱讀習慣，某校開展了為期一年的“弘揚傳統文化，閱讀經典名著”活動. 活動后，為了解閱讀情況，學校統計了甲、乙兩組各10名學生的閱讀量（單位：本），統計結果用莖葉圖記錄如下，乙組記錄中有一個數據模糊，無法確認，在圖中以a表示.
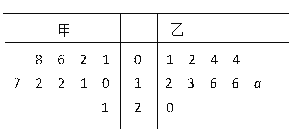
（Ⅰ）若甲組閱讀量的平均值大于乙組閱讀量的平均值，求圖中a的所有可能取值；
（Ⅱ）將甲、乙兩組中閱讀量超過15本的學生稱為“閱讀達人”. 設
，現從所有的“閱讀達人”里任取2人，求至少有1人來自甲組的概率；
（Ⅲ）記甲組閱讀量的方差為
. 若在甲組中增加一個閱讀量為10的學生，并記新得到的甲組閱讀量的方差為
，試比較，的大小.（結論不要求證明）
（注：
，其中
為數據
的平均數）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某綠色有機水果店中一款有機草莓味道鮮甜，店家每天以每斤
元的價格從農場購進適量草莓，然后以每斤
元的價格出售，如果當天賣不完，剩下的草莓由果汁廠以每斤
元的價格回收.
（1）若水果店一天購進
斤草莓，求當天的利潤
（單位：元）關于當天需求量
（單位：斤，
）的函數解析式；
（2）水果店記錄了
天草莓的日需求量（單位：斤），整理得下表：
日需求量 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
頻數 | 14 | 22 | 14 | 16 | 15 | 13 | 6 |
①假設水果店在這天內每天購進斤草莓，求這天的日利潤（單位：元）的平均數；
②若水果店一天購進斤草莓，以天記錄的各需求量的頻率作為各需求量發生的概率，求當天的利潤不少于
元的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱ABC﹣A1B1C1中，點D、E、F分別為線段A1C1、AB、A1A的中點，A1A＝AC＝BC，∠ACB＝90°．求證：
（1）DE∥平面BCC1B1；
（2）EF⊥平面B1CE．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
