
【題目】已知函數![]()
(1)討論函數f(x)的極值點的個數;
(2)若f(x)有兩個極值點x1、x2,證明:f(x1)+f(x2)>3-4ln2.
【答案】(Ⅰ)(ⅰ)![]() 時,
時,![]() 僅有一個極值點;(ⅱ) 當
僅有一個極值點;(ⅱ) 當![]() 時,
時,![]() 無極值點;
無極值點;
(ⅲ)當![]() 時,
時,![]() 有兩個極值點.(Ⅱ)詳見解析
有兩個極值點.(Ⅱ)詳見解析
【解析】試題(Ⅰ)先求導數,再確定導函數零點情況,這需分類討論:一次與二次的討論,二次中有根與無根的討論,兩根情況分相等、一正一負、兩不等正根,最后根據對應情況確定導函數符號變化規律,確定對應極值點個數;(Ⅱ)由(Ⅰ)先確定![]() 有兩個極值點時,
有兩個極值點時,![]() 的取值范圍,以及
的取值范圍,以及![]() 滿足條件,再化簡
滿足條件,再化簡![]() 為
為![]() 的函數,最后根據導數確定對應函數單調性,根據單調性證明不等式.
的函數,最后根據導數確定對應函數單調性,根據單調性證明不等式.
試題解析:解:(Ⅰ)由![]() 得,
得,
![]()
(ⅰ)![]() 時,
時,![]() ,
,![]()
所以![]() 取得極小值,
取得極小值,![]() 是
是![]() 的一個極小值點.
的一個極小值點.
(ⅱ)![]() 時,
時,![]() ,令
,令![]() ,得
,得![]()
顯然,![]() ,所以
,所以![]() ,
,
![]() 在
在![]() 取得極小值,
取得極小值,![]() 有一個極小值點.
有一個極小值點.
(ⅲ)![]() 時,
時,![]() 時,即
時,即![]() 在
在![]() 是減函數,
是減函數,![]() 無極值點.
無極值點.
當![]() 時,
時,![]() ,令
,令![]() ,得
,得![]()
當![]() 和
和![]() 時
時![]() ,
,![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 取得極小值,在
取得極小值,在![]() 取得極大值,所以
取得極大值,所以![]() 有兩個極值點.
有兩個極值點.
綜上可知:(ⅰ)![]() 時,
時,![]() 僅有一個極值點;
僅有一個極值點;
(ⅱ) 當![]() 時,
時,![]() 無極值點;
無極值點;
(ⅲ)當![]() 時,
時,![]() 有兩個極值點.
有兩個極值點.
(Ⅱ)由(Ⅰ)知,當且僅當![]() 時,
時,![]() 有極小值點
有極小值點![]() 和極大值點
和極大值點![]() ,且
,且
![]() 是方程
是方程![]() 的兩根,所以
的兩根,所以![]() ,
,
![]()
![]()
![]() ,
,
設![]() ,
,![]() ,
,
所以![]() 時,
時,![]() 是減函數,
是減函數,![]() ,則
,則![]()
所以![]() 得證.
得證.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)求![]() 的單調區間;
的單調區間;
(Ⅱ)求![]() 在區間
在區間![]() 上的最小值.
上的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】(Ⅰ)![]() .
.
令![]() ,得
,得![]() .
.

![]() 與
與![]() 的情況如上:
的情況如上:
所以,![]() 的單調遞減區間是
的單調遞減區間是![]() ,單調遞增區間是
,單調遞增區間是![]() .
.
(Ⅱ)當![]() ,即
,即![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() 在區間
在區間![]() 上的最小值為
上的最小值為![]() .
.
當![]() ,即
,即![]() 時,
時,
由(Ⅰ)知![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
所以![]() 在區間
在區間![]() 上的最小值為
上的最小值為![]() .
.
當![]() ,即
,即![]() 時,函數
時,函數![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() 在區間
在區間![]() 上的最小值為
上的最小值為![]() .
.
綜上,當![]() 時,
時,![]() 的最小值為
的最小值為![]() ;
;
當![]() 時,
時,![]() 的最小值為
的最小值為![]() ;
;
當![]() 時,
時,![]() 的最小值為
的最小值為![]() .
.
【題型】解答題
【結束】
19
【題目】已知拋物線![]() 的頂點在原點,焦點在坐標軸上,點
的頂點在原點,焦點在坐標軸上,點![]() 為拋物線
為拋物線![]() 上一點.
上一點.
(1)求![]() 的方程;
的方程;
(2)若點![]() 在
在![]() 上,過
上,過![]() 作
作![]() 的兩弦
的兩弦![]() 與
與![]() ,若
,若![]() ,求證: 直線
,求證: 直線![]() 過定點.
過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為奇函數,
為奇函數, ![]() 為偶函數,且
為偶函數,且![]() .
.
(1)求![]() 及
及![]() 的解析式及定義域;
的解析式及定義域;
(2)若關于![]() 的不等式
的不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
(3)如果函數![]() ,若函數
,若函數![]() 有兩個零點,求實數
有兩個零點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市100戶居民的月平均用電量(單位:度)以[160,180)[180,200)[200,220)[220,240)[240,260)[260,280)[280,300)分組的頻率分布直方圖如圖所示:
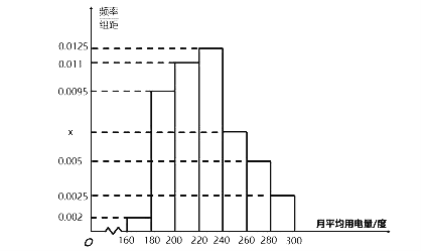
(1)求直方圖中![]() 的值;
的值;
(2)用分層抽樣的方法從[260,280)和[280,300)這兩組用戶中確定6人做隨訪,再從這6人中隨機抽取2人做問卷調查,則這2人來自不同組的概率是多少?
(3)求月平均用電量的眾數和中位數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】按文獻記載,《百家姓》成文于北宋初年,表1記錄了《百家姓》開頭的24大姓氏:
表1:
趙 | 錢 | 孫 | 李 | 周 | 吳 | 鄭 | 王 | 馮 | 陳 | 褚 | 衛 |
蔣 | 沈 | 韓 | 楊 | 朱 | 秦 | 尤 | 許 | 何 | 呂 | 施 | 張 |
表2記錄了2018年中國人口最多的前10大姓氏:
表2:
1:李 | 2:王 | 3:張 | 4:劉 | 5:陳 |
6:楊 | 7:趙 | 8:黃 | 9:周 | 10:吳 |
從《百家姓》開頭的24大姓氏中隨機選取1個姓氏,則這個姓氏是2018年中國人口最多的前10大姓氏的概率為_____________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() C的極坐標方程為
C的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)設![]() 分別交
分別交![]() 于點
于點![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,離心率為
,離心率為![]() ,過
,過![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,且
兩點,且![]() 的周長為
的周長為![]()
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 分別交于
分別交于![]() 兩點,且
兩點,且![]() ,試問點
,試問點![]() 到直線
到直線![]() 的距離是否為定值,證明你的結論.
的距離是否為定值,證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com