
【題目】某房地產商建有三棟樓宇![]() ,三樓宇間的距離都為2千米,擬準備在此三樓宇圍成的區域
,三樓宇間的距離都為2千米,擬準備在此三樓宇圍成的區域![]() 外建第四棟樓宇
外建第四棟樓宇![]() ,規劃要求樓宇
,規劃要求樓宇![]() 對樓宇
對樓宇![]() ,
,![]() 的視角為
的視角為![]() ,如圖所示,假設樓宇大小高度忽略不計.
,如圖所示,假設樓宇大小高度忽略不計.
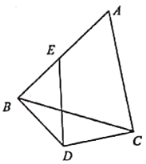
(1)求四棟樓宇圍成的四邊形區域![]() 面積的最大值;
面積的最大值;
(2)當樓宇![]() 與樓宇
與樓宇![]() ,
,![]() 間距離相等時,擬在樓宇
間距離相等時,擬在樓宇![]() ,
,![]() 間建休息亭
間建休息亭![]() ,在休息亭
,在休息亭![]() 和樓宇
和樓宇![]() ,
,![]() 間分別鋪設鵝卵石路
間分別鋪設鵝卵石路![]() 和防腐木路
和防腐木路![]() ,如圖,已知鋪設鵝卵石路、防腐木路的單價分別為
,如圖,已知鋪設鵝卵石路、防腐木路的單價分別為![]() ,
,![]() (單位:元千米,
(單位:元千米,![]() 為常數).記
為常數).記![]() ,求鋪設此鵝卵石路和防腐木路的總費用的最小值.
,求鋪設此鵝卵石路和防腐木路的總費用的最小值.
【答案】(1)圍成的四邊形區域![]() 的面積的最大值
的面積的最大值![]() 平方千米;(2)總費用的最小值
平方千米;(2)總費用的最小值![]() 元.
元.
【解析】
(1)由樓宇![]() 對樓宇
對樓宇![]() ,
,![]() 的視角為
的視角為![]() 得樓宇D在一段圓弧上,則
得樓宇D在一段圓弧上,則![]() 相等時,可得
相等時,可得![]() 最大,
最大,![]() 固定,計算此時四邊形
固定,計算此時四邊形![]() 的面積即可.
的面積即可.
(2)用![]() 表示出
表示出![]() ,
,![]() ,從而表示出鋪設此鵝卵石路和防腐木路的總費:
,從而表示出鋪設此鵝卵石路和防腐木路的總費:![]() ,再利用導數判斷
,再利用導數判斷![]() 的單調性,從而求得它的最小值,問題得解.
的單調性,從而求得它的最小值,問題得解.
(1)當且僅當:![]() 時,取得等號,所以
時,取得等號,所以![]() 的最大值為
的最大值為![]()
又因為四邊形![]() 的面積
的面積![]()
所以四邊形![]() 的面積的最大值為
的面積的最大值為![]() .
.
答:四棟樓宇圍成的四邊形區域![]() 的面積的最大值
的面積的最大值![]() 平方千米.
平方千米.
(2)當樓宇![]() 與樓宇
與樓宇![]() 間距離相等時
間距離相等時
由(1)得:![]()
則![]() ,又因為
,又因為![]() ,所以
,所以![]() ,因為等邊三角形
,因為等邊三角形![]()
所以![]() ,所以
,所以![]()
在![]() 中,
中,![]() ,所以
,所以![]()
![]() ,則
,則![]()
所以鋪設鵝卵石路和防腐木路的總費用
![]()
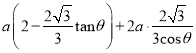
![]()
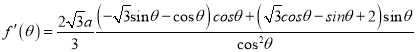
![]()
令![]()
因為![]() ,所以
,所以![]()
|
|
|
|
| - | 0 | + |
| ↘ | 極小值 | ↗ |
所以當![]() 時,
時,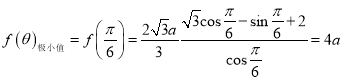
即:![]() 的最小值為
的最小值為![]()
答:鋪設此鵝卵石路和防腐木路的總費用的最小值![]() 元.
元.


科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),在以直角坐標系的原點
為參數),在以直角坐標系的原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸的極坐標系中,曲線
軸的正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(Ⅱ)若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
, ![]() 兩點,求
兩點,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知離心率為![]() 的橢圓
的橢圓![]() 的左頂點為
的左頂點為![]() ,左焦點為
,左焦點為![]() ,及點
,及點![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比數列.
成等比數列.
(1)求橢圓![]() 的方程;
的方程;
(2)斜率不為![]() 的動直線
的動直線![]() 過點
過點![]() 且與橢圓
且與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點,記
兩點,記![]() ,線段
,線段![]() 上的點
上的點![]() 滿足
滿足![]() ,試求
,試求![]() (
(![]() 為坐標原點)面積的取值范圍.
為坐標原點)面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在新型冠狀病毒疫情期間,商業活動受到很大影響某小型零售連鎖店總部統計了本地區50家加盟店2月份的零售情況,統計數據如圖所示.據估計,平均銷售收入比去年同期下降40%,則去年2月份這50家加盟店的平均銷售收入約為( )
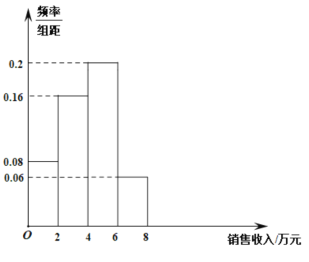
A.6.6萬元B.3.96萬元C.9.9萬元D.7.92萬元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從一批蘋果中,隨機抽取50個,其重量(單位:克)的頻數分布表如下:
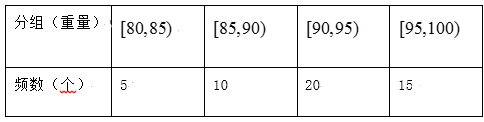
(1)根據頻數分布表計算蘋果的重量在![]() 的頻率;
的頻率;
(2)用分層抽樣的方法從重量在![]() 和
和![]() 的蘋果中共抽取4個,其中重量在
的蘋果中共抽取4個,其中重量在![]() 的有幾個?
的有幾個?
(3)在(2)中抽出的4個蘋果中,任取2個,寫出所有可能的結果,并求重量在![]() 和
和![]() 中各有1個的概率.
中各有1個的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設你有一筆資金,現有三種投資方案,這三種方案的回報如下:
方案一:每天回報40元;
方案二:第一天回報10元,以后每天比前一天多回報10元;
方案三:第一天回報0.4元,以后每天的回報比前一天翻一番.
現打算投資10天,三種投資方案的總收益分別為![]() ,
,![]() ,
,![]() ,則( )
,則( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() ,拋物線
,拋物線![]() ,點A是橢圓
,點A是橢圓![]() 與拋物線
與拋物線![]() 的交點,過點A的直線l交橢圓
的交點,過點A的直線l交橢圓![]() 于點B,交拋物線
于點B,交拋物線![]() 于M(B,M不同于A).
于M(B,M不同于A).
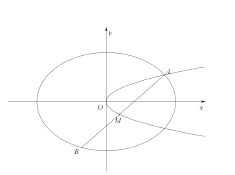
(Ⅰ)若![]() ,求拋物線
,求拋物線![]() 的焦點坐標;
的焦點坐標;
(Ⅱ)若存在不過原點的直線l使M為線段AB的中點,求p的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com