
【題目】已知橢圓![]() 過點
過點![]() ,
,![]() ,其上頂點到直線
,其上頂點到直線![]() 的距離為2,過點
的距離為2,過點![]() 的直線
的直線![]() 與
與![]() ,
,![]() 軸的交點分別為
軸的交點分別為![]() 、
、![]() ,且
,且![]() .
.
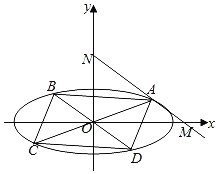
(1)證明:![]() 為定值;
為定值;
(2)如上圖所示,若![]() ,
,![]() 關于原點對稱,
關于原點對稱,![]() ,
,![]() 關于原點對稱,且
關于原點對稱,且![]() ,求四邊形
,求四邊形![]() 面積的最大值.
面積的最大值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)其上頂點![]() 到直線
到直線![]() 的距離為2,求出
的距離為2,求出![]() ,點
,點![]() 代入橢圓方程,可求出橢圓方程,設經過點
代入橢圓方程,可求出橢圓方程,設經過點![]() 的直線方程為:
的直線方程為:![]() ,可得
,可得![]() ,
,![]() .利用
.利用![]() ,可得
,可得![]() ,利用兩點之間的距離公式可得
,利用兩點之間的距離公式可得![]() ;
;
(2)由(1)得直線![]() 的方程為
的方程為![]() ,與橢圓方程聯立求出
,與橢圓方程聯立求出![]() ,由點到直線距離公式,求出
,由點到直線距離公式,求出![]() 到直線
到直線![]() 距離,求出四邊形
距離,求出四邊形![]() 面積的關于
面積的關于![]() 的表達式,結合
的表達式,結合![]() 關系,由基本不等式求出最大值.
關系,由基本不等式求出最大值.
(1)其上頂點![]() 到直線
到直線![]() 的距離為2,
的距離為2,
![]() ,解得
,解得![]() .
.
又橢圓![]() 過點
過點![]() ,
,
![]() ,解得
,解得![]() .
.
∴橢圓的標準方程為:![]() .
.
點![]() 在橢圓上,
在橢圓上,![]() .
.
設經過點![]() 的直線方程為:
的直線方程為:![]() ,
,
可得![]() ,
,![]() .
.
![]() ,
,![]() 即
即![]() .
.
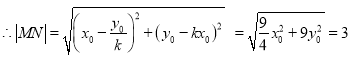 為定值.
為定值.
(2)由(1)得直線![]() 斜率為
斜率為![]() ,
,
![]() 方程為
方程為![]() ,
,
即![]() ,
,![]() ,
,
聯立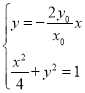 解得
解得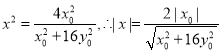 ,
,
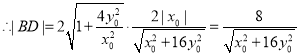 ,
,
點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,
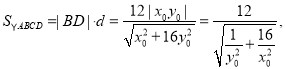
![]()
當且僅當![]() ,即
,即![]() 時,等號成立,
時,等號成立,
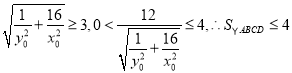 ,
,
四邊形![]() 面積的最大值為
面積的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】2022年北京冬奧會的申辦成功與“3億人上冰雪”口號的提出,將冰雪這個冷項目迅速炒“熱”.北京某綜合大學計劃在一年級開設冰球課程,為了解學生對冰球運動的興趣,隨機從該校一年級學生中抽取了100人進行調查,其中女生中對冰球運動有興趣的占![]() ,而男生有10人表示對冰球運動沒有興趣額.
,而男生有10人表示對冰球運動沒有興趣額.
(1)完成![]() 列聯表,并回答能否有
列聯表,并回答能否有![]() 的把握認為“對冰球是否有興趣與性別有關”?
的把握認為“對冰球是否有興趣與性別有關”?
有興趣 | 沒興趣 | 合計 | |
男 | 55 | ||
女 | |||
合計 |
(2)已知在被調查的女生中有5名數學系的學生,其中3名對冰球有興趣,現在從這5名學生中隨機抽取3人,求至少有2人對冰球有興趣的概率.
附表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左頂點為
的左頂點為![]() ,右焦點為
,右焦點為![]() ,斜率為1的直線與橢圓
,斜率為1的直線與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,其中
,其中![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設過點![]() 且與直線
且與直線![]() 平行的直線與橢圓
平行的直線與橢圓![]() 交于
交于![]() ,
,![]() 兩點,若點
兩點,若點![]() 滿足
滿足![]() ,且
,且![]() 與橢圓
與橢圓![]() 的另一個交點為
的另一個交點為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,直線
軸的正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)若射線![]() 的極坐標方程為
的極坐標方程為![]() (
(![]() ).設
).設![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() 與
與![]() 相交于點
相交于點![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑.
如圖,在陽馬![]() 中,側棱
中,側棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 為
為![]() 中點,點
中點,點![]() 在
在![]() 上,且
上,且![]() 平面
平面![]() ,連接
,連接![]() ,
, ![]() .
.
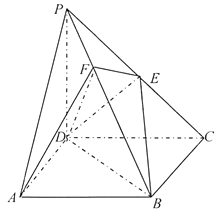
(Ⅰ)證明: ![]() 平面
平面![]() ;
;
(Ⅱ)試判斷四面體![]() 是否為鱉臑,若是,寫出其每個面的直角(只需寫出結論);若不是,說明理由;
是否為鱉臑,若是,寫出其每個面的直角(只需寫出結論);若不是,說明理由;
(Ⅲ)已知![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】波羅尼斯(古希臘數學家,的公元前262-190年)的著作《圓錐曲線論》是古代世界光輝的科學成果,它將圓錐曲線的性質網羅殆盡,幾乎使后人沒有插足的余地.他證明過這樣一個命題:平面內與兩定點距離的比為常數k(k>0,且k≠1)的點的軌跡是圓,后人將這個圓稱為阿波羅尼斯圓.現有橢圓![]() =1(a>b>0),A,B為橢圓的長軸端點,C,D為橢圓的短軸端點,動點M滿足
=1(a>b>0),A,B為橢圓的長軸端點,C,D為橢圓的短軸端點,動點M滿足![]() =2,△MAB面積的最大值為8,△MCD面積的最小值為1,則橢圓的離心率為( )
=2,△MAB面積的最大值為8,△MCD面積的最小值為1,則橢圓的離心率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正三棱柱![]() 各條棱的長度均相等,
各條棱的長度均相等,![]() 為
為![]() 的中點,
的中點,![]() 分別是線段
分別是線段![]() 和線段
和線段![]() 的動點(含端點),且滿足
的動點(含端點),且滿足![]() ,當
,當![]() 運動時,下列結論中不正確的是
運動時,下列結論中不正確的是

A. 在![]() 內總存在與平面
內總存在與平面![]() 平行的線段
平行的線段
B. 平面![]() 平面
平面![]()
C. 三棱錐![]() 的體積為定值
的體積為定值
D. ![]() 可能為直角三角形
可能為直角三角形
查看答案和解析>>
科目:高中數學 來源: 題型:
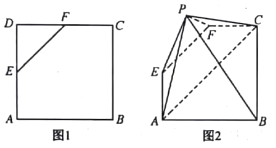
【題目】如圖1,在邊長為4的正方形![]() 中,
中,![]() 是
是![]() 的中點,
的中點,![]() 是
是![]() 的中點,現將三角形
的中點,現將三角形![]() 沿
沿![]() 翻折成如圖2所示的五棱錐
翻折成如圖2所示的五棱錐![]() .
.
(1)求證:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com