
【題目】已知函數![]() .
.
(Ⅰ)求曲線![]() 在點處的切線方程;
在點處的切線方程;
(Ⅱ)當![]() 時,求證:函數
時,求證:函數![]() 有且僅有一個零點;
有且僅有一個零點;
(Ⅲ)當![]() 時,寫出函數
時,寫出函數![]() 的零點的個數.(只需寫出結論)
的零點的個數.(只需寫出結論)
【答案】(Ⅰ)![]() ;(Ⅱ)證明見解析;(Ⅲ)當
;(Ⅱ)證明見解析;(Ⅲ)當![]() 時,
時, ![]() 有一個零點;當
有一個零點;當![]() 且
且![]() 時,
時, ![]() 有兩個零點.
有兩個零點.
【解析】試題分析:(Ⅰ)求得函數的導函數,得到![]() ,
, ![]() ,進而得到切線的方程.
,進而得到切線的方程.
(Ⅱ)當![]() 時,求得函數
時,求得函數![]() 的導數,得
的導數,得![]() ,則
,則![]() 為單調遞增函數,又由
為單調遞增函數,又由![]() ,進而得到
,進而得到![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增,所以函數
單調遞增,所以函數![]() 的最小值為
的最小值為![]() ,即可證明結論;
,即可證明結論;
(Ⅲ)根據函數的單調性和極值,可得當![]() 和
和![]() 且
且![]() 時時,
時時, ![]() 零點的個數.
零點的個數.
試題解析:
(Ⅰ)因為函數![]() ,所以
,所以![]()
故![]() ,
, ![]() , 曲線
, 曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]()
(Ⅱ)當![]() 時,令
時,令![]() ,則
,則![]()
故![]() 是
是![]() 上的增函數.
上的增函數.
由![]() ,故當
,故當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() .
.
即當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() .
.
故![]() 在
在![]() 單調遞減,在
單調遞減,在![]() 單調遞增.
單調遞增.
函數![]() 的最小值為
的最小值為![]() ,由
,由![]() ,故
,故![]() 有且僅有一個零點.
有且僅有一個零點.
(Ⅲ)當![]() 時,
時, ![]() 有一個零點;當
有一個零點;當![]() 且
且![]() 時,
時, ![]() 有兩個零點.
有兩個零點.


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:高中數學 來源: 題型:
【題目】如圖1, 在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為線段
為線段![]() 的中點. 將
的中點. 將![]() 沿
沿![]() 折起,使平面
折起,使平面![]()
![]() 平面
平面![]() ,得到幾何體
,得到幾何體![]() ,如圖2所示.
,如圖2所示.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在“新零售”模式的背景下,某大型零售公司為推廣線下分店,計劃在![]() 市的
市的![]() 區開設分店.為了確定在該區開設分店的個數,該公司對該市已開設分店的其他區的數據作了初步處理后得到下列表格.記
區開設分店.為了確定在該區開設分店的個數,該公司對該市已開設分店的其他區的數據作了初步處理后得到下列表格.記![]() 表示在各區開設分店的個數,
表示在各區開設分店的個數, ![]() 表示這
表示這![]() 個分店的年收入之和.
個分店的年收入之和.
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
(Ⅰ)該公司已經過初步判斷,可用線性回歸模型擬合![]() 與
與![]() 的關系,求
的關系,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(Ⅱ)假設該公司在![]() 區獲得的總年利潤
區獲得的總年利潤![]() (單位:百萬元)與
(單位:百萬元)與![]() 之間的關系為
之間的關系為![]() ,請結合(Ⅰ)中的線性回歸方程,估算該公司應在
,請結合(Ⅰ)中的線性回歸方程,估算該公司應在![]() 區開設多少個分店,才能使
區開設多少個分店,才能使![]() 區平均每個分店的年利潤最大?
區平均每個分店的年利潤最大?
參考公式:
![]() ,
, 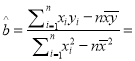
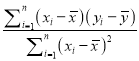 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來我國電子商務行業迎來發展的新機遇,2017年雙11全天交易額達到1682億元,為規范和評估該行業的情況,相關管理部門制定出針對電商的商品和服務的評價體系.現從評價系統中選出200次成功交易,并對其評價進行評價,對商品的好評率為0.6,對服務的好評率為0.75,其中對商品和服務都做出好評的交易為80次.
(1)完成關于商品和服務評價的![]() 列聯表,判斷能否在犯錯誤的概率不超過0.001的前提下,認為商品好評與服務好評有關?
列聯表,判斷能否在犯錯誤的概率不超過0.001的前提下,認為商品好評與服務好評有關?
(2)若將頻率視為概率,某人在該購物平臺上進行的3次購物中,設對商品和服務全為好評的次數為隨機變量![]() :
:
①求對商品和服務全為好評的次數![]() 的分布列;
的分布列;
②求![]() 的數學期望和方差.
的數學期望和方差.
附:臨界值表:

![]() 的觀測值:
的觀測值: 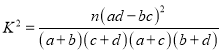 (其中
(其中![]() )
)
關于商品和服務評價的![]() 列聯表:
列聯表:

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2017·黃岡質檢)設等比數列{an}的各項均為正數,公比為q,前n項和為Sn.若對任意的n∈N*,有S2n<3Sn,則q的取值范圍是( )
A. (0,1] B. (0,2)
C. [1,2) D. (0, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學調查了某班全部![]() 名同學參加書法社團和演講社團的情況,數據如下表:(單位:人)
名同學參加書法社團和演講社團的情況,數據如下表:(單位:人)

(1)能否由![]() 的把握認為參加書法社團和參加演講社團有關?
的把握認為參加書法社團和參加演講社團有關?
(附: 
當![]() 時,有
時,有![]() 的把握說事件
的把握說事件![]() 與
與![]() 有關;當
有關;當![]() ,認為事件
,認為事件![]() 與
與![]() 是無關的)
是無關的)
(2)已知既參加書法社團又參加演講社團的![]() 名同學中,有
名同學中,有![]() 名男同學
名男同學![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 名女同學
名女同學![]() ,
, ![]() ,
, ![]() .現從這
.現從這![]() 名男同學和
名男同學和![]() 名女同學中各隨機選
名女同學中各隨機選![]() 人,求
人,求![]() 被選中且
被選中且![]() 未被選中的概率.
未被選中的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com