
【題目】已知圓![]() ,直線
,直線![]() 過點
過點![]() 且與圓
且與圓![]() 相切 .
相切 .
(I)求直線![]() 的方程;
的方程;
(II)如圖,圓![]() 與
與![]() 軸交于
軸交于![]() 兩點,點
兩點,點![]() 是圓
是圓![]() 上異于
上異于![]() 的任意一點,過點
的任意一點,過點![]() 且與
且與![]() 軸垂直的直線為
軸垂直的直線為![]() ,直線
,直線![]() 交直線
交直線![]() 于點
于點![]() ,直線
,直線![]() 交直線
交直線![]() 于點
于點![]() ,求證:以
,求證:以![]() 為直徑的圓
為直徑的圓![]() 與
與![]() 軸交于定點
軸交于定點![]() ,并求出點
,并求出點![]() 的坐標 .
的坐標 .

【答案】(1)![]() .
.
(2)證明見解析;定點![]() 或
或![]() .
.
【解析】
(1)由已知中直線![]() 過點
過點![]() ,我們可以設出直線的點斜式方程,化為一般式方程后,代入點到直線距離公式,根據直線與圓相切,圓心到直線的距離等于半徑,可以求出k的值,進而得到直線
,我們可以設出直線的點斜式方程,化為一般式方程后,代入點到直線距離公式,根據直線與圓相切,圓心到直線的距離等于半徑,可以求出k的值,進而得到直線![]() 的方程;
的方程;
(2)由已知我們易求出P,Q兩個點的坐標,設出M點的坐標,我們可以得到點P與Q的坐標,進而得到以![]() 為直徑的圓
為直徑的圓![]() 的方程,根據圓的方程即可判斷結論.
的方程,根據圓的方程即可判斷結論.
(Ⅰ)由題意得,直線![]() 的斜率存在.
的斜率存在.
設直線![]() 的方程為
的方程為![]() .
.
因為直線![]() 與圓
與圓![]() 相切,
相切,
所以![]() .
.
所以![]() .
.
所以直線方程為![]() .
.
(Ⅱ)由題意得,點![]() ,點
,點![]() .
.
設點![]() ,則
,則![]() .
.
直線![]() 的方程為
的方程為![]() .
.
所以直線![]() 與直線
與直線![]() 的交點為點
的交點為點![]() .
.
直線![]() 的方程為
的方程為![]() .
.
所以直線![]() 與直線
與直線![]() 的交點為點
的交點為點![]() .
.
設點![]() .
.
則![]() ,
,![]() .
.
因為以![]() 為直徑的圓
為直徑的圓![]() 與
與![]() 軸交于定點
軸交于定點![]() ,
,
所以![]()
解得![]() .
.
所以定點![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】設|θ|< ![]() ,n為正整數,數列{an}的通項公式an=sin
,n為正整數,數列{an}的通項公式an=sin ![]() tannθ,其前n項和為Sn
tannθ,其前n項和為Sn
(1)求證:當n為偶函數時,an=0;當n為奇函數時,an=(﹣1) ![]() tannθ;
tannθ;
(2)求證:對任何正整數n,S2n= ![]() sin2θ[1+(﹣1)n+1tan2nθ].
sin2θ[1+(﹣1)n+1tan2nθ].
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某連鎖經營公司所屬5個零售店某月的銷售額和利潤額資料如表所示:
商店名稱 | A | B | C | D | E |
銷售額(x)/千萬元 | 3 | 5 | 6 | 7 | 9 |
利潤額(y)/百萬元 | 2 | 3 | 3 | 4 | 5 |
(1)畫出銷售額和利潤額的散點圖.
(2)若銷售額和利潤額具有相關關系,用最小二乘法計算利潤額y對銷售額x的回歸直線方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =
=![]() ,
,![]() =
=![]() -
-![]()
![]() .
.
(3)若獲得利潤是4.5百萬元時估計銷售額是多少(千萬元)?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市計劃按月訂購一種酸奶,每天進貨量相同,進貨成本每瓶4元,售價每瓶6元,未售出的酸奶降價處理,以每瓶2元的價格當天全部處理完.根據往年銷售經驗,每天需求量與當天最高氣溫(單位:℃)有關.如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區間![]() ,需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
,需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
最高 氣溫 | [10, 15) | [15, 20) | [20, 25) | [25, 30) | [30, 35) | [35, 40) |
天數 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高氣溫位于各區間的頻率代替最高氣溫位于該區間的概率.
(1)求六月份這種酸奶一天的需求量X(單位:瓶)的分布列.
(2)設六月份一天銷售這種酸奶的利潤為Y(單位:元),當六月份這種酸奶一天的進貨量n(單位:瓶)為多少時,Y的數學期望達到最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據某電子商務平臺的調查統計顯示,參與調查的1000位上網購物者的年齡情況如圖顯示. 
(1)已知[30,40)、[40,50)、[50,60)三個年齡段的上網購物者人數成等差數列,求a,b的值.
(2)該電子商務平臺將年齡在[30,50)之間的人群定義為高消費人群,其他的年齡段定義為潛在消費人群,為了鼓勵潛在消費人群的消費,該平臺決定發放代金券,高消費人群每人發放50元的代金券,潛在消費人群每人發放100元的代金券,現采用分層抽樣的方式從參與調查的1000位上網購者中抽取10人,并在這10人中隨機抽取3人進行回訪,求此三人獲得代金券總和X的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面ABCD是菱 形,PA=PB,且側面PAB⊥平面ABCD,點E是AB的中點.
中,底面ABCD是菱 形,PA=PB,且側面PAB⊥平面ABCD,點E是AB的中點.
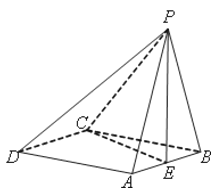
(1)求證:PE⊥AD;
(2)若CA=CB,求證:平面PEC⊥平面PAB.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在棱長為![]() 的正方體
的正方體![]() 中,
中,![]() ,
,![]() 分別是
分別是![]() 和
和![]() 的中點.
的中點.

(![]() )求異面直線
)求異面直線![]() 與
與![]() 所成角的余弦值.
所成角的余弦值.
(![]() )在棱
)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com