
【題目】已知函數![]()
![]() ,函數
,函數![]() 的圖象經過
的圖象經過![]() ,其導函數
,其導函數![]() 的圖象是斜率為
的圖象是斜率為![]() ,過定點
,過定點![]() 的一條直線.
的一條直線.
(1)討論![]()
![]() 的單調性;
的單調性;
(2)當![]() 時,不等式
時,不等式![]() 恒成立,求整數
恒成立,求整數![]() 的最小值.
的最小值.
【答案】(1)當![]() 時,
時,![]() 在
在![]() 上為減函數;
上為減函數;
當![]() 時,
時,![]() 在
在![]() 上為減函數,在
上為減函數,在![]() 上為增函數.
上為增函數.
(2)2
【解析】
對![]() 求導,得到
求導,得到![]() ,按
,按![]() 和
和![]() 進行分類討論,利用導函數的正負,得到
進行分類討論,利用導函數的正負,得到![]() 的單調性;(2)根據題意先得到
的單調性;(2)根據題意先得到![]() ,然后得到
,然后得到![]() 的解析式,設
的解析式,設![]() ,按
,按![]() 和
和![]() 分別討論,利用
分別討論,利用![]() 得到
得到![]() 的單調性和最大值,然后研究其最大值恒小于等于
的單調性和最大值,然后研究其最大值恒小于等于![]() 時,整數
時,整數![]() 的最小值.
的最小值.
(1)函數![]() 的定義域是
的定義域是![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上為減函數,
上為減函數,
當![]() 時,令
時,令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,
,![]() 為減函數,
為減函數,
當![]() 時,
時,![]() ,
,![]() 為增函數,
為增函數,
綜上,當![]() 時,
時,![]() 在
在![]() 上為減函數;
上為減函數;
當![]() 時,
時,![]() 在
在![]() 上為減函數,在
上為減函數,在![]() 上為增函數.
上為增函數.
(2)根據題意,![]() ,
,
設![]() ,代入
,代入![]() ,可得
,可得![]() ,
,
令![]()
![]() ,
,
所以![]()
![]() .
.
當![]() 時,因為
時,因為![]() ,所以
,所以![]() .
.
所以![]() 在
在![]() 上是單調遞增函數,
上是單調遞增函數,
又因為![]()
![]() ,
,
所以關于x的不等式![]() 不能恒成立.
不能恒成立.
當![]() 時,
時,![]()
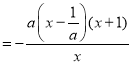 ,
,
令![]() ,得
,得![]() .
.
所以當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() ,
,
因此函數![]() 在
在![]() 上是增函數,在
上是增函數,在![]() 上是減函數.
上是減函數.
故函數![]() 的最大值為
的最大值為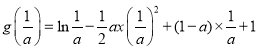
![]() .
.
令![]() ,因為
,因為![]()
![]() ,
,
又因為![]() 在
在![]() 上是減函數.
上是減函數.
所以當![]() 時,
時,![]() .
.
所以整數![]() 的最小值為
的最小值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】對于![]() ,若數列
,若數列![]() 滿足
滿足![]() ,則稱這個數列為“K數列”.
,則稱這個數列為“K數列”.
(Ⅰ)已知數列:1,m+1,m2是“K數列”,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)是否存在首項為-1的等差數列![]() 為“K數列”,且其前n項和
為“K數列”,且其前n項和![]() 滿足
滿足
![]() ?若存在,求出
?若存在,求出![]() 的通項公式;若不存在,請說明理由;
的通項公式;若不存在,請說明理由;
(Ⅲ)已知各項均為正整數的等比數列![]() 是“K數列”,數列
是“K數列”,數列![]() 不是“K數列”,若
不是“K數列”,若![]() ,試判斷數列
,試判斷數列![]() 是否為“K數列”,并說明理由.
是否為“K數列”,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義在![]() 上的函數
上的函數![]() ,若函數
,若函數![]() 滿足:
滿足:
①在區間![]() 上單調遞減,②存在常數p,使其值域為
上單調遞減,②存在常數p,使其值域為![]() ,則稱函數
,則稱函數![]() 是函數
是函數![]() 的“逼進函數”.
的“逼進函數”.
(1)判斷函數![]() 是不是函數
是不是函數![]() 的“逼進函數”;
的“逼進函數”;
(2)求證:函數![]() 不是函數
不是函數![]() ,的“逼進函數”
,的“逼進函數”
(3)若![]() 是函數
是函數![]() 的“逼進函數”,求a的值.
的“逼進函數”,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司有l000名員工,其中男性員工400名,采用分層抽樣的方法隨機抽取100名員工進行5G手機購買意向的調查,將計劃在今年購買5G手機的員工稱為“追光族”,計劃在明年及明年以后才購買5G手機的員工稱為“觀望者”調查結果發現抽取的這100名員工中屬于“追光族”的女性員工和男性員工各有20人.
(Ⅰ)完成下列![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為該公司員工屬于“追光族”與“性別”有關;
的把握認為該公司員工屬于“追光族”與“性別”有關;
屬于“追光族” | 屬于“觀望者” | 合計 | |
女性員工 | |||
男性員工 | |||
合計 | 100 |
(Ⅱ)已知被抽取的這l00名員工中有6名是人事部的員工,這6名中有3名屬于“追光族”現從這6名中隨機抽取3名,求抽取到的3名中恰有1名屬于“追光族”的概率.
附: ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以平面直角坐標系中的坐標原點為極點,![]() 軸的正半抽為極軸,建立極坐標系,曲線
軸的正半抽為極軸,建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() ,直線
,直線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數).
為參數).
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的傾斜角
的傾斜角![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com