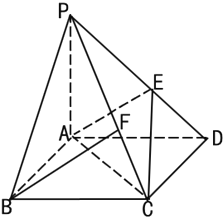
【題目】如圖，底面是平行四邊形的四棱錐
中，
，
，且
，若
平面
，則
______.
【答案】
【解析】
取棱PC上的點F，使
，取棱PD上的點M使
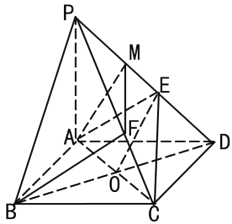
，連接BD．設BD∩AC＝O．結(jié)合平行四邊形的性質(zhì)及三角形中位線定理及面面平行的判定定理可得平面BMF∥平面AEC，進而由面面平行的性質(zhì)得到BF∥平面AEC．
存在點F滿足使BF∥平面AEC
理由如下：
取棱PC上的點F，使，取棱PD上的點M使，則E為MD中點，
連接BD．設BD∩AC＝O．
連接BM，OE．
∵=
,F為PC的中點，E是MD的中點，
∴MF∥EC，BM∥OE．
∵MF平面AEC，CE平面AEC，BM平面AEC，OE平面AEC，
∴MF∥平面AEC，BM∥平面AEC．
∵MF∩BM＝M，
∴平面BMF∥平面AEC．
又BF平面BMF，
∴BF∥平面AEC．
故答案為：
科目：高中數(shù)學 來源： 題型：
【題目】某企業(yè)生產(chǎn)的某種產(chǎn)品被檢測出其中一項質(zhì)量指標存在問題．該企業(yè)為了檢查生產(chǎn)該產(chǎn)品的甲、乙兩條流水線的生產(chǎn)情況，隨機地從這兩條流水線上生產(chǎn)的大量產(chǎn)品中各抽取50件產(chǎn)品作為樣本，測出它們的這一項質(zhì)量指標值．若該項質(zhì)量指標值落在(195，210]內(nèi)，則為合格品，否則為不合格品．表1是甲流水線樣本的頻數(shù)分布表，圖1是乙流水線樣本的頻率分布直方圖
圖1：乙流水線樣本頻率分布直方圖
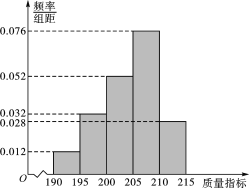
表1：甲流水線樣本頻數(shù)分布表
質(zhì)量指標值 | 頻數(shù) |
(190，195] | 9 |
(195，200] | 10 |
(200，205] | 17 |
(205，210] | 8 |
(210，215] | 6 |
（1）根據(jù)圖1，估計乙流水線生產(chǎn)產(chǎn)品該質(zhì)量指標值的中位數(shù)和平均數(shù)（估算平均數(shù)時，同一組中的數(shù)據(jù)用該組區(qū)間的中點值為代表）；
（2）若將頻率視為概率，某個月內(nèi)甲、乙兩條流水線均生產(chǎn)了5000件產(chǎn)品，則甲，乙兩條流水線分別生產(chǎn)出的不合格品約多少件？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知拋物線
的方程
，焦點為
，已知點
在上，且點到點的距離比它到
軸的距離大1.
（1）試求出拋物線的方程；
（2）若拋物線上存在兩動點
（在對稱軸兩側(cè)），滿足
（
為坐標原點），過點作直線交于
兩點，若
，線段
上是否存在定點
，使得
恒成立？若存在，請求出的坐標，若不存在，請說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設P為橢圓
1（a＞b＞0）上任一點，F1、F2為橢圓的焦點，|PF1|+|PF2|＝4，離心率為
．
（1）求橢圓的方程；
（2）若直線l：y＝kx+m（≠0）與橢圓交于A、B兩點，若線段AB的中點C的直線y
x上，O為坐標原點．求△OAB的面積S的最大值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設函數(shù)
在
上有意義，實數(shù)
和
滿足
，若在區(qū)間
上不存在最小值，則稱在上具有性質(zhì)
.
（1）當
，且在區(qū)間
上具有性質(zhì)時，求常數(shù)
的取值范圍；
（2）已知
，且當
，
，判斷在區(qū)間
上是否具有性質(zhì)，請說明理由：
（3）若對于滿足的任意實數(shù)和，在上具有性質(zhì)時，且對任意
，當
時有：
，證明：當
時，
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知數(shù)列
滿足：
（常數(shù)
），
.數(shù)列
滿足：
.
（1）求
的值；
（2）求出數(shù)列的通項公式；
（3）問：數(shù)列的每一項能否均為整數(shù)？若能，求出k的所有可能值；若不能，請說明理由.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
，函數(shù)
的圖象經(jīng)過
，其導函數(shù)
的圖象是斜率為
，過定點
的一條直線.
（1）討論的單調(diào)性；
（2）當
時，不等式
恒成立，求整數(shù)
的最小值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
