
【題目】對任意![]() ,都存在
,都存在![]() ,使得
,使得![]() ,其中
,其中![]() 為自然對數的底數,則實數
為自然對數的底數,則實數![]() 的取值范圍是______
的取值范圍是______
【答案】![]()
【解析】
令![]() ,根據函數單調性可得f(x)∈[﹣1,e2],然后令g(x)=ax﹣ex,由x1≠x2,g(x1)=g(x2),可知y=mlnm﹣m與y=g(x)的圖象有2個交點,結合函數單調性即可求解.
,根據函數單調性可得f(x)∈[﹣1,e2],然后令g(x)=ax﹣ex,由x1≠x2,g(x1)=g(x2),可知y=mlnm﹣m與y=g(x)的圖象有2個交點,結合函數單調性即可求解.
令![]() ,則
,則![]() ,
,
當![]() 時,f′(x)=lnx<0,∴f(x)單調遞減,
時,f′(x)=lnx<0,∴f(x)單調遞減,
當1<x<e2,f′(x)=lnx>0,∴f(x)單調遞增,
∵![]() ,故函數f(x)的值域為
,故函數f(x)的值域為![]() .
.
令g(x)=ax﹣ex,則g′(x)=a﹣ex,且x1≠x2,g(x1)=g(x2),
①當a≤0時,g′(x)=a﹣ex<0恒成立,∴g(x)在R上單調遞減,
與x1≠x2,g(x1)=g(x2),矛盾
②當a>0時,當x>lna時,g′(x)=a﹣ex<0,∴函數g(x)單調遞減,
當x<lna時,g′(x)=a﹣ex>0,∴函數g(x)單調遞增,
∵當x→﹣∞時,g(x)→﹣∞,當x→+∞時,g(x)→﹣∞且
g(x)max=g(lna)=alna﹣a,
∴當x1≠x2時,若g(x1)=g(x2)=mlnm﹣m,
則y=mlnm與y=g(x)有2個不同的交點,
∴alna﹣a>e2=e2lne2﹣e2,又a>0
由f(x)的單調性可得a>e2,
∴實數a的取值范圍為:(e2,+∞).
故答案為:(e2,+∞)


科目:高中數學 來源: 題型:
【題目】空中有一氣球,在它的正西方A點測得它的仰角為45°,同時在它南偏東60°的B點,測得它的仰角為30°,已知A、B兩點間的距離為107米,這兩個觀測點均離地1米,則測量時氣球離地的距離是_____米.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學舉行一次“環保知識競賽”,全校學生參加了這次競賽.為了解本次競賽成績情況,從中抽取了部分學生的成績(得分取正整數,滿分為![]() 分)作為樣本進行統計,請根據下面尚未完成并有局部污損的樣本的頻率分布表和頻率分布直方圖(如圖所示)解決下列問題:
分)作為樣本進行統計,請根據下面尚未完成并有局部污損的樣本的頻率分布表和頻率分布直方圖(如圖所示)解決下列問題:
(Ⅰ)寫出![]() ,
, ![]() ,
, ![]() ,
, ![]() 的值.
的值.
(Ⅱ)在選取的樣本中,從競賽成績是![]() 分以上(含
分以上(含![]() 分)的同學中隨機抽取
分)的同學中隨機抽取![]() 名同學到廣場參加環保知識的志愿宣傳活動,求所抽取的
名同學到廣場參加環保知識的志愿宣傳活動,求所抽取的![]() 名同學來自同一組的概率.
名同學來自同一組的概率.
(Ⅲ)在(Ⅱ)的條件下,設![]() 表示所抽取的
表示所抽取的![]() 名同學中來自第
名同學中來自第![]() 組的人數,求
組的人數,求![]() 的分布列及其數學期望.
的分布列及其數學期望.
組別 | 分組 | 頻數 | 頻率 |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
合計 |
|
|

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ( x R ,且 e 為自然對數的底數).
( x R ,且 e 為自然對數的底數).
⑴ 判斷函數 f x 的單調性與奇偶性;
⑵是否存在實數 t ,使不等式![]() 對一切的 x R 都成立?若存在,求出 t 的值,若 不存在說明理由.
對一切的 x R 都成立?若存在,求出 t 的值,若 不存在說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大豆是我國主要的農作物之一,因此,大豆在農業發展中占有重要的地位,隨著農業技術的不斷發展,為了使大豆得到更好的種植,就要進行超級種培育研究.某種植基地培育的“超級豆”種子進行種植測試:選擇一塊營養均衡的可種植![]() 株的實驗田地,每株放入三粒“超級豆”種子,且至少要有一粒種子發芽這株豆苗就能有效成活,每株豆成活苗可以收成大豆
株的實驗田地,每株放入三粒“超級豆”種子,且至少要有一粒種子發芽這株豆苗就能有效成活,每株豆成活苗可以收成大豆![]() .已知每粒豆苗種子成活的概率為
.已知每粒豆苗種子成活的概率為![]() (假設種子之間及外部條件一致,發芽相互沒有影響).
(假設種子之間及外部條件一致,發芽相互沒有影響).
(Ⅰ)求恰好有3株成活的概率;
(Ⅱ)記成活的豆苗株數為![]() ,收成為
,收成為![]() ,求隨機變量
,求隨機變量![]() 分布列及
分布列及![]() 數學期望
數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
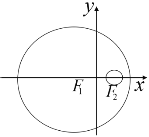
【題目】如圖,已知圓![]() 的方程為
的方程為![]() ,圓
,圓![]() 的方程為
的方程為![]() ,若動圓
,若動圓![]() 與圓
與圓![]() 內切,與圓
內切,與圓![]() 外切.
外切.
(Ⅰ)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過直線![]() 上的點
上的點![]() 作圓
作圓![]() 的兩條切線,設切點分別是
的兩條切線,設切點分別是![]() ,
,![]() ,若直線
,若直線![]() 與軌跡
與軌跡![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com