【題目】設函數
（a>0且a≠1）是奇函數．
（1）求常數k的值；
（2）若已知f（1）=
，且函數
在區間[1，+∞]）上的最小值為—2，求實數m的值．
【答案】（1）
；（2）
．
【解析】
試題（1）函數
的定義域為R，∵函數（a>0且a≠1）是奇函數
∴f（0）=k－1=0，∴k=1．
（2）∵f（1）=
，∴
=，解得a=3或
∵a>0且a≠1，∴a=3
g（x）=32x+3-2x－2m（3x－3-x）= （3x－3-x）2－2m（3x－3-x）+2 （x≥1）
令3x－3-x=t （t≥），則y=t2－2mt+2=（t—m）2—m2+2）
當m≥時，
=—m2+2=－2，解得m=2或m=-2，舍去
當m<時，= （）2－2m×+2=－2，解得m=
∴m=．
試題解析：（1）函數的定義域為R
∵函數（a>0且a≠1）是奇函數
∴f（0）=k－1=0
∴k=1
（2）∵f（1）=
∴=，解得a=3或
∵a>0且a≠1
∴a=3
g（x）=32x+3-2x－2m（3x－3-x）= （3x－3-x）2－2m（3x－3-x）+2 （x≥1）
令3x－3-x=t （t≥）
則y=t2－2mt+2=（t—m）2—m2+2
當m≥時，=—m2+2=－2，解得m=2或m=-2，舍去
當m<時，= （）2－2m×+2=－2，解得m=
∴m=
科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足：a1＝1，且當n2時，
（1）若＝1，證明數列{a2n1}是等差數列；
（2）若＝2.①設
，求數列{bn}的通項公式；②設
，證明：對于任意的p，m N *，當p m，都有
Cm.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列四個命題：①任意兩條直線都可以確定一個平面；②若兩個平面有3個不同的公共點，則這兩個平面重合；③直線a，b，c，若a與b共面，b與c共面，則a與c共面；④若直線l上有一點在平面α外，則l在平面α外.其中錯誤命題的個數是（ ）
A.1B.2C.3D.4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖①，有一個長方體形狀的敞口玻璃容器，底面是邊長為20cm的正方形，高為30cm，內有20cm深的溶液．現將此容器傾斜一定角度
（圖②），且傾斜時底面的一條棱始終在桌面上（圖①、②均為容器的縱截面）．
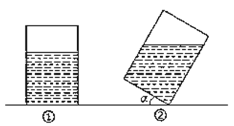
（1）要使傾斜后容器內的溶液不會溢出，角的最大值是多少？
（2）現需要倒出不少于
的溶液，當
時，能實現要求嗎？請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，正方體ABCD﹣A′B′C′D′的棱長為1，E，F分別是棱AA′，CC′的中點，過直線E，F的平面分別與棱BB′、DD′交于M，N，設BM＝x，x∈[0，1]，給出以下四個命題：
①平面MENF⊥平面BDD′B′；
②當且僅當x＝
時，四邊形MENF的面積最小；
③四邊形MENF周長L＝f（x），x∈[0，1]是單調函數；
④四棱錐C′﹣MENF的體積V＝h（x）為常函數；
以上命題中假命題的序號為（ ）
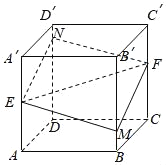
A. ①④B. ②C. ③D. ③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系中，以原點為極點，x軸的正半軸為極軸建立極坐標系，已知曲線
，直線l的參數方程為：
（t為參數），直線l與曲線C分別交于
兩點.
（1）寫出曲線C和直線l的普通方程；
（2）若點
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某調查機構對全國互聯網行業進行調查統計，得到整個互聯網行業從業者年齡分布餅狀圖和90后從事互聯網行業者崗位分布圖（90后指1990年及以后出生，80后指1980-1989年之間出生，80前指1979年及以前出生），則下列結論中不一定正確的是（ ）
整個互聯網行業從業者年齡分布餅狀圖 90后從事互聯網行業者崗位分布圖
A.互聯網行業從業人員中90后占一半以上
B.互聯網行業中從事技術崗位的人數90后比80后多
C.互聯網行業中從事設計崗位的人數90后比80前多
D.互聯網行業中從事市場崗位的90后人數不足總人數的10%
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
