
【題目】設函數![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求函數
,求函數![]() 的單調區間;
的單調區間;
(2)若曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 平行.
平行.
①求![]() ,
,![]() 的值;
的值;
②求實數![]() 的取值范圍,使得
的取值范圍,使得![]() 對
對![]() 恒成立.
恒成立.
【答案】(1)![]() 的單調增區間為
的單調增區間為![]() ,單調減區間為
,單調減區間為![]() (2)①
(2)①![]() ②
②![]()
【解析】
(1)求出函數的導數,通過解關于導函數的不等式,求出函數的單調區間即可;
(2)①求出g(x)的導數,得到關于a,b的方程組,解出即可;
②問題轉化為g(x)﹣k(x2﹣x)>0對x∈(0,+∞)恒成立.令F(x)=g(x)﹣k(x2﹣x),求出函數的導數,通過討論k的范圍,求出函數的單調區間,從而確定k的范圍即可.
(1)當![]() ,
,![]() 時,
時,![]() ,
,
則![]() .當
.當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() ;
;
所以![]() 的單調增區間為
的單調增區間為![]() ,單調減區間為
,單調減區間為![]() .
.
(2)①因為![]() ,
,
所以![]() ,依題設有
,依題設有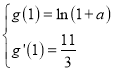 ,即
,即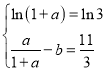 .
.
解得![]() .
.
②![]() ,
,![]() .
.
![]() 對
對![]() 恒成立,即
恒成立,即![]() 對
對![]() 恒成立.
恒成立.
令![]() ,則有
,則有![]() .
.
當![]() 時,當
時,當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調遞增.
上單調遞增.
所以![]() ,即當
,即當![]() 時,
時,![]() ;
;
當![]() 時,當
時,當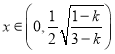 時,
時,![]() ,所以
,所以![]() 在
在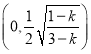 上單調遞減,故當
上單調遞減,故當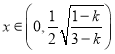 時,
時,![]() ,即當
,即當![]() 時,
時,![]() 不恒成立.
不恒成立.
綜上,![]() .
.


科目:高中數學 來源: 題型:
【題目】某土特產超市為預估2020年元旦期間游客購買土特產的情況,對2019年元旦期間的90位游客購買情況進行統計,得到如下人數分布表.
購買金額(元) |
|
|
|
|
|
|
人數 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根據以上數據完成![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為購買金額是否少于60元與性別有關.
的把握認為購買金額是否少于60元與性別有關.
不少于60元 | 少于60元 | 合計 | |
男 | 40 | ||
18 | |||
合計 |
(2)為吸引游客,該超市推出一種優惠方案,購買金額不少于60元可抽獎3次,每次中獎概率為![]() (每次抽獎互不影響,且
(每次抽獎互不影響,且![]() 的值等于人數分布表中購買金額不少于60元的頻率),中獎1次減5元,中獎2次減10元,中獎3次減15元.若游客甲計劃購買80元的土特產,請列出實際付款數
的值等于人數分布表中購買金額不少于60元的頻率),中獎1次減5元,中獎2次減10元,中獎3次減15元.若游客甲計劃購買80元的土特產,請列出實際付款數![]() (元)的分布列并求其數學期望.
(元)的分布列并求其數學期望.
附:參考公式和數據: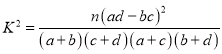 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列判斷正確的是( )
A.若隨機變量![]() 服從正態分布
服從正態分布![]() ,
,![]() ,則
,則![]() ;
;
B.已知直線![]() 平面
平面![]() ,直線
,直線![]() 平面
平面![]() ,則“
,則“![]() ”是“
”是“![]() ”的充分不必要條件;
”的充分不必要條件;
C.若隨機變量![]() 服從二項分布:
服從二項分布:![]() ,則
,則![]() ;
;
D.![]() 是
是![]() 的充分不必要條件.
的充分不必要條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義在區間![]() 上的函數
上的函數![]() ,若同時滿足:
,若同時滿足:
(Ⅰ)若存在閉區間![]() ,使得任取
,使得任取![]() ,都有
,都有![]() (
(![]() 是常數);
是常數);
(Ⅱ)對于![]() 內任意
內任意![]() ,當
,當![]() ,時總有
,時總有![]() 恒成立,則稱函數
恒成立,則稱函數![]() 為“平底型”函數.
為“平底型”函數.
(1)判斷函數![]() 和
和![]() 是否是“平底型”函數?簡要說明理由;
是否是“平底型”函數?簡要說明理由;
(2)設![]() 是(1)中的“平底型”函數,若不等式
是(1)中的“平底型”函數,若不等式![]() 對一切
對一切![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)函數![]() 是區間
是區間![]() 上的“平底型”函數,求
上的“平底型”函數,求![]() 和
和![]() 滿足的條件,并說明理由.
滿足的條件,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設滿足以下兩個條件的有窮數列![]() 為
為![]() 階“期待數列”:①
階“期待數列”:①![]() ;②
;②![]() .
.
(1)若等比數列![]() 為
為![]() 階“期待數列”
階“期待數列”![]() ,求公比
,求公比![]() ;
;
(2)若一個等差數列![]() 既是
既是![]() 階“期待數列”又是遞增數列
階“期待數列”又是遞增數列![]() ,求該數列的通項公式;
,求該數列的通項公式;
(3)記![]() 階“期待數列”
階“期待數列” ![]() 的前
的前![]() 項和為
項和為![]() ,求證;數列
,求證;數列![]() 不能為
不能為![]() 階“期待數列”.
階“期待數列”.
查看答案和解析>>
科目:高中數學 來源: 題型:
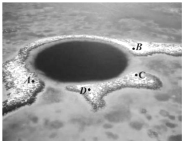
【題目】海洋藍洞是地球罕見的自然地理現象,被喻為“地球留給人類保留宇宙秘密的最后遺產”,我國擁有世界上最深的海洋藍洞,若要測量如圖所示的藍洞的口徑![]() ,
,![]() 兩點間的距離,現在珊瑚群島上取兩點
兩點間的距離,現在珊瑚群島上取兩點![]() ,
,![]() ,測得
,測得![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() 兩點的距離為___.
兩點的距離為___.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com