
【題目】在實(shí)數(shù)集R中定義一種運(yùn)算“⊙”,具有性質(zhì):①對(duì)任意a、b∈R,a⊙b=b⊙a(bǔ);②a⊙0=a;③對(duì)任意a、b∈R,(a⊙b)⊙c=(ab)⊙c+(a⊙c)+(b⊙c)﹣2c,則函數(shù)f(x)=x⊙ ![]() 的最小值是( )
的最小值是( )
A.2
B.3
C.![]()
D.![]()
【答案】B
【解析】解:根據(jù)題意,得 f(x)=x⊙ ![]() =(x⊙
=(x⊙ ![]() )⊙0=0⊙(x
)⊙0=0⊙(x ![]() )+(x⊙0)+(
)+(x⊙0)+( ![]() ⊙0)﹣2×0=1+x+
⊙0)﹣2×0=1+x+ ![]()
即f(x)=1+x+ ![]() ,
,
∵x>0,可得x+ ![]() ≥2,當(dāng)且僅當(dāng)x=1時(shí)等號(hào)成立,由此可得函數(shù)f(x)的最小值為f(1)=3.
≥2,當(dāng)且僅當(dāng)x=1時(shí)等號(hào)成立,由此可得函數(shù)f(x)的最小值為f(1)=3.
故選:B
【考點(diǎn)精析】認(rèn)真審題,首先需要了解函數(shù)的最值及其幾何意義(利用二次函數(shù)的性質(zhì)(配方法)求函數(shù)的最大(小)值;利用圖象求函數(shù)的最大(小)值;利用函數(shù)單調(diào)性的判斷函數(shù)的最大(小)值).


| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)f(x)=(x﹣1)ex﹣kx2(k∈R).
(1)當(dāng)k=1時(shí),求函數(shù)f(x)的單調(diào)區(qū)間;
(2)當(dāng) ![]() 時(shí),求函數(shù)f(x)在[0,k]上的最大值M.
時(shí),求函數(shù)f(x)在[0,k]上的最大值M.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an} 中,a1=1,a2= ![]() ,且
,且 ![]() (n=2,3,4,…)
(n=2,3,4,…)
(1)求a3、a4的值;
(2)設(shè)bn= ![]() (n∈N*),試用bn表示bn+1并求{bn} 的通項(xiàng)公式;
(n∈N*),試用bn表示bn+1并求{bn} 的通項(xiàng)公式;
(3)設(shè)cn= ![]() (n∈N*),求數(shù)列{cn}的前n項(xiàng)和Sn .
(n∈N*),求數(shù)列{cn}的前n項(xiàng)和Sn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
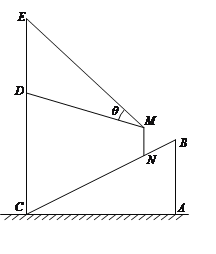
【題目】某商場在一部向下運(yùn)行的手扶電梯終點(diǎn)的正上方豎直懸掛一幅廣告畫.如圖,該電梯的高![]() 為
為![]() 米,它所占水平地面的長
米,它所占水平地面的長![]() 為
為![]() 米.該廣告畫最高點(diǎn)
米.該廣告畫最高點(diǎn)![]() 到地面的距離為
到地面的距離為![]() 米,最低點(diǎn)
米,最低點(diǎn)![]() 到地面距離
到地面距離![]() 米.假設(shè)某人眼睛到腳底的距離
米.假設(shè)某人眼睛到腳底的距離![]() 為
為![]() 米,他豎直站在此電梯上觀看
米,他豎直站在此電梯上觀看![]() 視角為
視角為![]() .
.
(Ⅰ)設(shè)此人到直線![]() 的距離為
的距離為![]() 米,試用含
米,試用含![]() 的表達(dá)式表示
的表達(dá)式表示![]() ;
;
(Ⅱ)此人到直線![]() 的距離為多少米時(shí),視角
的距離為多少米時(shí),視角![]() 最大?
最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù) ![]() 的部分圖象如圖所示,則下列結(jié)論錯(cuò)誤的是( )
的部分圖象如圖所示,則下列結(jié)論錯(cuò)誤的是( ) 
A.![]()
B.函數(shù)f(x)在 ![]() 上單調(diào)遞增
上單調(diào)遞增
C.函數(shù)f(x)的一條對(duì)稱軸是 ![]()
D.為了得到函數(shù)f(x)的圖象,只需將函數(shù)y=2cosx的圖象向右平移 ![]() 個(gè)單位
個(gè)單位
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若函數(shù)f(x)=ax2﹣(2a+1)x+a+1對(duì)于任意a∈[﹣1,1],都有f(x)<0,則實(shí)數(shù)x的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某投資公司計(jì)劃投資A,B兩種金融產(chǎn)品,根據(jù)市場調(diào)查與預(yù)測,A產(chǎn)品的利潤y1與投資金額x的函數(shù)關(guān)系為y1=18﹣ ![]() ,B產(chǎn)品的利潤y2與投資金額x的函數(shù)關(guān)系為y2=
,B產(chǎn)品的利潤y2與投資金額x的函數(shù)關(guān)系為y2= ![]() (注:利潤與投資金額單位:萬元).
(注:利潤與投資金額單位:萬元).
(1)該公司已有100萬元資金,并全部投入A,B兩種產(chǎn)品中,其中x萬元資金投入A產(chǎn)品,試把A,B兩種產(chǎn)品利潤總和表示為x的函數(shù),并寫出定義域;
(2)在(1)的條件下,試問:怎樣分配這100萬元資金,才能使公司獲得最大利潤?其最大利潤為多少萬元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
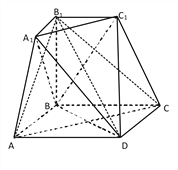
【題目】如圖所示的幾何體是由棱臺(tái)![]() 和棱錐
和棱錐![]() 拼接而成的組合體,其底面四邊形
拼接而成的組合體,其底面四邊形![]() 是邊長為
是邊長為![]() 的菱形,且
的菱形,且![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() .
.
(1)求證:平面![]()
![]() 平面
平面![]()
![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=4sin2( ![]() +
+ ![]() )sinx+(cosx+sinx)(cosx﹣sinx)﹣1.
)sinx+(cosx+sinx)(cosx﹣sinx)﹣1.
(1)化簡f(x);
(2)常數(shù)ω>0,若函數(shù)y=f(ωx)在區(qū)間 ![]() 上是增函數(shù),求ω的取值范圍;
上是增函數(shù),求ω的取值范圍;
(3)若函數(shù)g(x)= ![]() 在
在 ![]() 的最大值為2,求實(shí)數(shù)a的值.
的最大值為2,求實(shí)數(shù)a的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com