
【題目】已知函數f(x)=4sin2( ![]() +
+ ![]() )sinx+(cosx+sinx)(cosx﹣sinx)﹣1.
)sinx+(cosx+sinx)(cosx﹣sinx)﹣1.
(1)化簡f(x);
(2)常數ω>0,若函數y=f(ωx)在區間 ![]() 上是增函數,求ω的取值范圍;
上是增函數,求ω的取值范圍;
(3)若函數g(x)= ![]() 在
在 ![]() 的最大值為2,求實數a的值.
的最大值為2,求實數a的值.
【答案】
(1)解:f(x)=2[1﹣cos( ![]() +x)]sinx+cos2x﹣sin2x﹣1=(2+2sinx)sinx+1﹣2sin2x﹣1=2sinx
+x)]sinx+cos2x﹣sin2x﹣1=(2+2sinx)sinx+1﹣2sin2x﹣1=2sinx
(2)解:∵f(ωx)=2sinωx,由 ![]() ≤ωx≤
≤ωx≤ ![]() ,解得﹣
,解得﹣ ![]() +
+ ![]() ≤x≤
≤x≤ ![]() +
+ ![]() ,
,
∴f(ωx)的遞增區間為[﹣ ![]() +
+ ![]() ,
, ![]() +
+ ![]() ],k∈Z.∵f(ωx)在[﹣
],k∈Z.∵f(ωx)在[﹣ ![]() ,
, ![]() ]上是增函數,
]上是增函數,
∴當k=0時,有 ![]() ,∴
,∴ 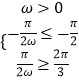 ,解得
,解得 ![]() ,
,
∴ω的取值范圍是(0, ![]() ]
]
(3)解:g(x)=sin2x+asinx﹣acosx﹣ ![]() a﹣1,令sinx﹣cosx=t,則sin2x=1﹣t2,
a﹣1,令sinx﹣cosx=t,則sin2x=1﹣t2,
∴y=1﹣t2+at﹣ ![]() a﹣1=﹣(t﹣
a﹣1=﹣(t﹣ ![]() )2+
)2+ ![]() ﹣
﹣ ![]() ,∵t=sinx﹣cosx=
,∵t=sinx﹣cosx= ![]() sin(x﹣
sin(x﹣ ![]() ),
),
∵x∈[﹣ ![]() ,
, ![]() ],∴x﹣
],∴x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],∴
],∴ ![]() .
.
① 當 ![]() <﹣
<﹣ ![]() ,即a<﹣2
,即a<﹣2 ![]() 時,ymax=﹣(-
時,ymax=﹣(- ![]() ﹣
﹣ ![]() )2+
)2+ ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() a﹣
a﹣ ![]() ﹣2.
﹣2.
令﹣ ![]() a﹣
a﹣ ![]() ﹣2=2,解得a=﹣
﹣2=2,解得a=﹣ ![]() (舍).
(舍).
②當﹣ ![]() ≤
≤ ![]() ≤1,即﹣2
≤1,即﹣2 ![]() ≤a≤2時,ymax=
≤a≤2時,ymax= ![]() ﹣
﹣ ![]() ,令
,令 ![]() ,解得a=﹣2或a=4(舍).
,解得a=﹣2或a=4(舍).
③當 ![]() ,即a>2時,在t=1處
,即a>2時,在t=1處 ![]() ,由
,由 ![]() 得a=6.
得a=6.
因此,a=﹣2或a=6
【解析】(1)使用降次公式和誘導公式化簡4sin2( ![]() +
+ ![]() ),使用平方差公式和二倍角公式化簡(cosx+sinx)(cosx﹣sinx);(2)求出f(ωx)的包含0的增區間U,令[﹣
),使用平方差公式和二倍角公式化簡(cosx+sinx)(cosx﹣sinx);(2)求出f(ωx)的包含0的增區間U,令[﹣ ![]() ,
, ![]() ]U,列出不等式組解出ω;(3)求出g(x)解析式,判斷g(x)的最大值,列方程解出a.
]U,列出不等式組解出ω;(3)求出g(x)解析式,判斷g(x)的最大值,列方程解出a.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】在實數集R中定義一種運算“⊙”,具有性質:①對任意a、b∈R,a⊙b=b⊙a;②a⊙0=a;③對任意a、b∈R,(a⊙b)⊙c=(ab)⊙c+(a⊙c)+(b⊙c)﹣2c,則函數f(x)=x⊙ ![]() 的最小值是( )
的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2cosxsin(x+ ![]() )﹣
)﹣ ![]() sin2x+sinxcosx.
sin2x+sinxcosx. 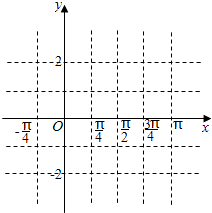
(1)當x∈[0, ![]() ]時,求f(x)的值域;
]時,求f(x)的值域;
(2)用五點法在圖中作出y=f(x)在閉區間[﹣ ![]() ,
, ![]() ]上的簡圖;
]上的簡圖;
(3)說明f(x)的圖象可由y=sinx的圖象經過怎樣的變化得到?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某正弦交流電的電壓v(單位V)隨時間t(單位:s)變化的函數關系是v=120 ![]() sin(100πt﹣
sin(100πt﹣ ![]() ),t∈[0,+∞).
),t∈[0,+∞).
(1)求該正弦交流電電壓v的周期、頻率、振幅;
(2)若加在霓虹燈管兩端電壓大于84V時燈管才發光,求在半個周期內霓虹燈管點亮的時間?( 取 ![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了促進學生的全面發展,鄭州市某中學重視學生社團文化建設,現用分層抽樣的方法從“話劇社”,“創客社”,“演講社”三個金牌社團中抽取6人組成社團管理小組,有關數據見表(單位:人):
社團名稱 | 成員人數 | 抽取人數 |
話劇社 | 50 | a |
創客社 | 150 | b |
演講社 | 100 | c |
(1)求a,b,c的值;
(2)若從“話劇社”,“創客社”,“演講社”已抽取的6人中任意抽取2人擔任管理小組組長,求這2人來自不同社團的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
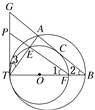
【題目】如圖所示,兩圓內切于點T,大圓的弦AB切小圓于點C.TA,TB與小圓分別相交于點E,F.FE的延長線交兩圓的公切線TP于點P.
求證:(1) ![]() =
=![]() ;
;
(2)AC·PF=BC·PT.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠生產的產品在出廠前都要做質量檢測,每一件一等品都能通過檢測,每一件二等品通過檢測的概率為![]() .現有10件產品,其中6件是一等品,4件是二等品.
.現有10件產品,其中6件是一等品,4件是二等品.
(1)隨機選取1件產品,求能夠通過檢測的概率;
(2)隨機選取3件產品,其中一等品的件數記為![]() ,求
,求![]() 的分布列及數學期望..
的分布列及數學期望..
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com