
【題目】某重點中學將全部高一新生分成A,B兩個成績相當(成績的均值、方差都相同)的級部,A級部采用傳統(tǒng)形式的教學方式,B級部采用新型的基于信息化的自主學習教學方式.期末考試后分別從兩個級部中各隨機抽取100名學生的數學成績進行統(tǒng)計,得到如下數據:
A級部教學 成績分組 |
|
|
|
|
|
|
頻數 | 18 | 23 | 29 | 23 | 6 | 1 |
B級部教學 成績分組 |
|
|
|
|
|
|
頻數 | 8 | 16 | 24 | 28 | 21 | 3 |
若成績不低于130分者為“優(yōu)秀”.
根據上表數據分別估計A,B兩個級部“優(yōu)秀”的概率;
(2)填寫下面的列聯(lián)表,并根據列聯(lián)表判斷是否有99%的把握認為“優(yōu)秀”與教學方式有關?
是否優(yōu)秀 級部 | 優(yōu)秀 | 不優(yōu)秀 | 合計 |
A級部 | |||
B級部 | |||
合計 |
(3)根據上表數據完成下面的頻率分布直方圖,并根據頻率分布直方圖,分別求出A,B兩個級部的中位數的估計值(精確到![]() );請根據以上計算結果初步分析A,B兩個級部的教學成績的優(yōu)劣.
);請根據以上計算結果初步分析A,B兩個級部的教學成績的優(yōu)劣.

附表:
|
|
|
|
|
|
|
|
|
|
|
|
附: 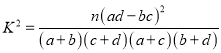
【答案】(1)![]() ;(2)見解析;(3) 見解析.
;(2)見解析;(3) 見解析.
【解析】試題分析:(1)根據表格中數據,利用古典概型概率公式可估計![]() 兩個級部“優(yōu)秀”的概率;(2)先根據表格中數據填寫列聯(lián)表,利用公式
兩個級部“優(yōu)秀”的概率;(2)先根據表格中數據填寫列聯(lián)表,利用公式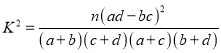 ,求得
,求得![]() ,從而可得結果;(3) 設
,從而可得結果;(3) 設![]() 級部的數學成績的中位數為
級部的數學成績的中位數為![]() ,由
,由![]() ,解得
,解得![]() 分,同理可得
分,同理可得![]() 級部的數學成績的中位數為
級部的數學成績的中位數為![]() ,比較中位數大小可初步分析
,比較中位數大小可初步分析![]() 兩個級部的教學成績的優(yōu)劣.
兩個級部的教學成績的優(yōu)劣.
試題解析:(1)A級部“優(yōu)秀”的概率的估計值為![]() ,B級部“優(yōu)秀”的概率的估計值為
,B級部“優(yōu)秀”的概率的估計值為![]() ;
;
(2)
是否優(yōu)秀 級部 | 優(yōu)秀 | 不優(yōu)秀 | 合計 |
A級部 | 7 | 93 | 100 |
B級部 | 24 | 76 | 100 |
合計 | 31 | 169 | 200 |
由列聯(lián)表可知, ![]() 的觀測值
的觀測值
![]() ,
,
所以有99%的把握認為“優(yōu)秀”與教學方式有關;
(3)
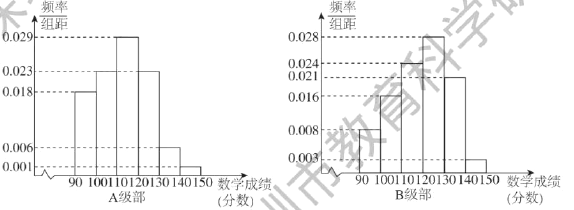
設A級部的數學成績的中位數為![]() ,
,
則![]() ,
,
解得![]() 分.
分.
設B級部的數學成績的中位數為![]() ,
,
則![]() ,
,
解得![]() 分.
分.
根據以上計算結果可知,①B級部數學成績的“優(yōu)秀”率大于A級部數學成績的“優(yōu)秀”率;②根據獨立性檢驗的結果有99%的把握認為“優(yōu)秀”與教學方式有關;③從A,B兩個級部的數學成績的中位數的估計值看,B級部的數據大于A級部的數據,故初步分析B級部的數學成績優(yōu)于A級部的數學成績.


 同步學典一課多練系列答案
同步學典一課多練系列答案 經典密卷系列答案
經典密卷系列答案 金牌課堂練系列答案
金牌課堂練系列答案 三新快車金牌周周練系列答案
三新快車金牌周周練系列答案科目:高中數學 來源: 題型:
【題目】下列命題中,真命題是( )
A. 設![]() ,則
,則![]() 為實數的充要條件是
為實數的充要條件是![]() 為共軛復數;
為共軛復數;
B. “直線![]() 與曲線C相切”是“直線
與曲線C相切”是“直線![]() 與曲線C只有一個公共點”的充分不必要條件;
與曲線C只有一個公共點”的充分不必要條件;
C. “若兩直線![]() ,則它們的斜率之積等于
,則它們的斜率之積等于![]() ”的逆命題;
”的逆命題;
D. ![]() 是R上的可導函數,“若
是R上的可導函數,“若![]() 是
是![]() 的極值點,則
的極值點,則![]() ”的否命題.
”的否命題.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在
是定義在![]() 上的奇函數,滿足
上的奇函數,滿足![]() ,當
,當![]() 時,有
時,有![]() .
.
(1)求實數![]() 的值;
的值;
(2)求函數![]() 在區(qū)間
在區(qū)間![]() 上的解析式,并利用定義證明證明其在該區(qū)間上的單調性;
上的解析式,并利用定義證明證明其在該區(qū)間上的單調性;
(3)解關于![]() 的不等式
的不等式![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校選派甲、乙、丙、丁、戊5名學生代表學校參加市級“演講”和“詩詞”比賽,下面是他們的一段對話.甲說:“乙參加‘演講’比賽”;乙說:“丙參加‘詩詞’比賽”;丙說“丁參加‘演講’比賽”;丁說:“戊參加‘詩詞’比賽”;戊說:“丁參加‘詩詞’比賽”.
已知這5個人中有2人參加“演講”比賽,有3人參加“詩詞”比賽,其中有2人說的不正確,且參加“演講”的2人中只有1人說的不正確.根據以上信息,可以確定參加“演講”比賽的學生是
A. 甲和乙 B. 乙和丙 C. 丁和戊 D. 甲和丁
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在![]() 中,
中,![]() ,且
,且![]() .
.
(1)求角![]() 的大小;
的大小;
(2)設數列![]() 滿足
滿足![]() ,前
,前![]() 項和為
項和為![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】試題分析:
(1)由題意結合三角形內角和為![]() 可得
可得![]() .由余弦定理可得
.由余弦定理可得![]() ,,結合勾股定理可知
,,結合勾股定理可知![]() 為直角三角形,
為直角三角形,![]() ,
,![]() .
.
(2)結合(1)中的結論可得![]()
![]() .則
.則![]()
![]() ,
,![]() 據此可得關于實數k的方程
據此可得關于實數k的方程![]() ,解方程可得
,解方程可得![]() ,則
,則![]() 或
或![]() .
.
試題解析:
(1)由已知![]() ,又
,又![]() ,所以
,所以![]() .又由
.又由![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() 為直角三角形,
為直角三角形,![]() ,
,![]() .
.
(2)![]()
![]() .
.
所以![]()
![]()
![]() ,
,![]() 由
由![]() ,得
,得
![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() 或
或![]() .
.
【題型】解答題
【結束】
18
【題目】已知點![]() 是平行四邊形
是平行四邊形![]() 所在平面外一點,如果
所在平面外一點,如果![]() ,
,![]() ,
,![]() .(1)求證:
.(1)求證:![]() 是平面
是平面![]() 的法向量;
的法向量;
(2)求平行四邊形![]() 的面積.
的面積.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com