
【題目】設數列![]() 的前
的前![]() 項和為
項和為![]() ,
, ![]() ,
, ![]() (
(![]() ).
).
(1)求數列![]() 的通項公式;
的通項公式;
(2)設![]() ,求數列
,求數列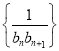 的前
的前![]() 項和
項和![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1) 由![]() 可得
可得![]() ,兩式相減得,
,兩式相減得, ![]() ,即
,即![]() (
(![]() ,
, ![]() ),從而可得數列
),從而可得數列![]() 為等比數列,進而可得數列
為等比數列,進而可得數列![]() 的通項公式;(2)由(1)得,
的通項公式;(2)由(1)得, ![]() ,
, ![]() ,利用裂項相消法求解即可.
,利用裂項相消法求解即可.
試題解析:(1) ![]() ,
,
由![]() ①,可得
①,可得![]() ②.
②.
①-②得, ![]() ,即
,即![]() (
(![]() ,
, ![]() ).
).
故![]() .
.
當![]() 時,
時, ![]() ,所以
,所以![]() .
.
(1)由(1)得, ![]() ,
,
所以![]() .
.
所以![]() .
.
【方法點晴】本題主要考查等比數列的定義與通項公式,以及裂項相消法求數列的和,屬于中檔題. 裂項相消法是最難把握的求和方法之一,其原因是有時很難找到裂項的方向,突破這一難點的方法是根據式子的結構特點,常見的裂項技巧:(1) ![]() ;(2)
;(2) ![]()
![]() ; (3)
; (3)![]() ;(4)
;(4)![]()
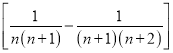 ;此外,需注意裂項之后相消的過程中容易出現丟項或多項的問題,導致計算結果錯誤.
;此外,需注意裂項之后相消的過程中容易出現丟項或多項的問題,導致計算結果錯誤.


科目:高中數學 來源: 題型:
【題目】已知點A(0,﹣2),橢圓E: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,F是橢圓的焦點,直線AF的斜率為
,F是橢圓的焦點,直線AF的斜率為 ![]() ,O為坐標原點.
,O為坐標原點.
(Ⅰ)求E的方程;
(Ⅱ)設過點A的直線l與E相交于P,Q兩點,當△OPQ的面積最大時,求l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=1g(1﹣x)的值域為(﹣∞,0),則函數f(x)的定義域為( )
A.[0,+∞]
B.(0,1)
C.[﹣9,+∞)
D.[﹣9,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設公差不為零的等差數列{an}的前5項的和為55,且a2 , ![]() ﹣9成等比數列.
﹣9成等比數列.
(1)求數列{an}的通項公式.
(2)設數列bn= ![]() ,求證:數列{bn}的前n項和Sn<
,求證:數列{bn}的前n項和Sn< ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 且Sn+an=4,n∈N*
(1)求數列{an}的通項公式;
(2)已知cn=2n+3(n∈N*),記dn=cn+logCan(C>0,C≠1),是否存在這樣的常數C,使得數列{dn}是常數列,若存在,求出C的值;若不存在,請說明理由.
(3)若數列{bn},對于任意的正整數n,均有 ![]() 成立,求證:數列{bn}是等差數列.
成立,求證:數列{bn}是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是根據調查結果繪制的兩幅不完整的統計圖,請你根據統計圖提供的信息解答以下問題:
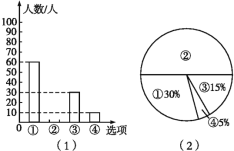
(1)本次一共調查了多少名學生.(2)在圖(1)中將②對應的部分補充完整.
(3)若該校有3 000名學生,你估計全校有多少名學生平均每天參加體育活動的時間在0.5時以下?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商品一年內出廠價格在6元的基礎上按月份隨正弦曲線波動,已知3月份達到最高價格8元,7月份價格最低為4元,該商品在商店內的銷售價格在8元基礎上按月份隨正弦曲線波動,5月份銷售價格最高為10元,9月份銷售價最低為6元,假設商店每月購進這種商品m件,且當月銷完,你估計哪個月份盈利最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場對顧客實行購物優惠活動,規定一次購物付款總額:
(1)如果不超過200元,則不給予優惠;
(2)如果超過200元但不超過500元,則按標價給予9折優惠;
(3)如果超過500元,其500元內的按第(2)條給予優惠,超過500元的部分給予7折優惠.
某人單獨購買A,B商品分別付款168元和423元,假設他一次性購買A,B兩件商品,則應付款是
A. 413.7元 B. 513.7元 C. 546.6元 D. 548.7元
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com