
【題目】已知函數![]() (
(![]() ).
).
(1)若![]() 為
為![]() 的極值點,求實數
的極值點,求實數![]() 的值;
的值;
(2)若![]() 在
在![]() 上是單調增函數,求實數
上是單調增函數,求實數![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,方程
時,方程![]() 有實根,求實數
有實根,求實數![]() 的最大值.
的最大值.
【答案】(1)0;(2)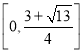 ;(3)0.
;(3)0.
【解析】
(1)根據![]() 建立關于a的方程求出a的值.
建立關于a的方程求出a的值.
(2)本小題實質是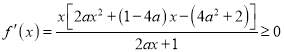 在區間
在區間![]() 上恒成立,
上恒成立,
進一步轉化為![]() 在區間
在區間![]() 上恒成立,
上恒成立,
然后再討論a=0和![]() 兩種情況研究.
兩種情況研究.
(2)![]() 時,方程
時,方程![]() 可化為,
可化為,![]() ,
,
問題轉化為![]() 在
在![]() 上有解,
上有解,
利用導數研究g(x)的單調區間極值最值,從而求出值域,問題得解.
(1)![]()
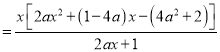 .
.
因為![]() 為
為![]() 的極值點,所以
的極值點,所以![]() .
.
即![]() ,解得
,解得![]() .
.
又當![]() 時,
時,![]() ,從而
,從而![]() 的極值點成立.
的極值點成立.
(2)因為![]() 在區間
在區間![]() 上為增函數,
上為增函數,
所以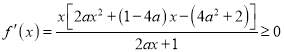 在區間
在區間![]() 上恒成立.
上恒成立.
①當![]() 時,
時,![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 上為增函數,故
上為增函數,故![]() ,符合題意.
,符合題意.
②當![]() 時,由函數
時,由函數![]() 的定義域可知,必須有
的定義域可知,必須有![]() 對
對![]() 恒成立,故只能
恒成立,故只能![]() ,所以
,所以![]() 對
對
![]() 上恒成立.
上恒成立.
令![]() ,其對稱軸為
,其對稱軸為![]() ,
,
因為![]() 所以
所以![]() ,從而
,從而![]() 上恒成立,只要
上恒成立,只要![]() 即可,
即可,
因為![]()
![]() ,
,
解得![]() .因為
.因為![]() ,所以
,所以![]() .
.
綜上所述,![]() 的取值范圍為
的取值范圍為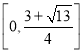 .
.
(3)若![]() 時,方程
時,方程![]() 可化為,
可化為,![]() .
.
問題轉化為![]() 在
在![]() 上有解,
上有解,
即求函數![]() 的值域.
的值域.
因為![]() ,令
,令![]() ,
,
則![]() ,
,
所以當![]() 時,
時,![]() ,從而
,從而![]() 在
在![]() 上為增函數,
上為增函數,
當![]() 時,
時,![]() ,從而
,從而![]() 在
在![]() 上為減函數,
上為減函數,
因此![]() .
.
而![]() ,故
,故![]() ,
,
因此當![]() 時,
時,![]() 取得最大值0.
取得最大值0.


 53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源: 題型:
【題目】如圖,在多面體![]() 中,梯形
中,梯形![]() 與平行四邊形
與平行四邊形![]() 所在平面互相垂直,
所在平面互相垂直, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)判斷線段![]() 上是否存在點
上是否存在點![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求 出
?若存在,求 出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校100名學生的數學測試成績的頻率分布直方圖如圖所示,分數不低于a即為優秀,如果優秀的人數為20,則a的估計值是( )
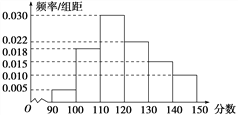
A. 130 B. 140 C. 133 D. 137
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知學校高三年級有學生1000名,經調查研究,其中750名同學經常參加體育鍛煉(稱為A類同學),另外250名同學不經常參加體育鍛煉(稱為B類同學). 現用分層抽樣方法(按A類、B類分兩層)從該年級學生中共抽查100名同學,測得這100名同學的身高(單位:![]() )頻率分布直方圖如圖:
)頻率分布直方圖如圖:
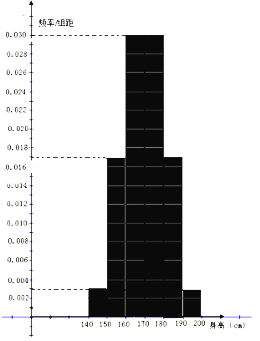
(Ⅰ)以同一組數據常用該組區間的中點值(例如區間![]() 的中點值為165)作為代表,計算這100名學生身高數據的平均值;
的中點值為165)作為代表,計算這100名學生身高數據的平均值;
(Ⅱ)如果以身高不低于![]() 作為達標的標準,對抽取的100名學生,得到以下列聯表:
作為達標的標準,對抽取的100名學生,得到以下列聯表:
身高達標 | 身高不達標 | 總計 | |
積極參加體育鍛煉 | 40 | ||
不積極參加體育鍛煉 | 15 | ||
總計 | 100 |
完成上表,并判斷是否有![]() 的把握認為體育鍛煉與身高達標有關系(
的把握認為體育鍛煉與身高達標有關系(![]() 值精確到0.01)?
值精確到0.01)?
參考公式: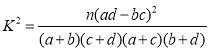
參考數據:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨機抽取了40輛汽車在經過路段上某點時的車速(km/h),現將其分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如圖所示的頻率分布直方圖.
,后得到如圖所示的頻率分布直方圖.
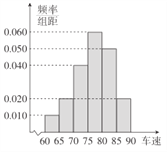
(Ⅰ)現有某汽車途經該點,則其速度低于80km/h的概率約是多少?
(Ⅱ)根據直方圖可知,抽取的40輛汽車經過該點的平均速度約是多少?
(Ⅲ)在抽取的40輛且速度在![]() (km/h)內的汽車中任取2輛,求這2輛車車速都在
(km/h)內的汽車中任取2輛,求這2輛車車速都在![]() (km/h)內的概率.
(km/h)內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為激發學生學習的興趣,老師上課時在黑板上寫出三個集合:![]()
![]() ;然后叫甲、乙、丙三位同學到講臺上,并將“
;然后叫甲、乙、丙三位同學到講臺上,并將“![]() ”中的數告訴了他們,要求他們各用一句話來描述,以便同學們能確定該數,以下是甲、乙、丙三位同學的描述:
”中的數告訴了他們,要求他們各用一句話來描述,以便同學們能確定該數,以下是甲、乙、丙三位同學的描述:
甲:此數為小于6的正整數;乙:A是B成立的充分不必要條件;
丙:A是C成立的必要不充分條件
若老師評說這三位同學都說得對,則“![]() ”中的數為 。
”中的數為 。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,已知M,N分別為線段BB1,A1C的中點,MN⊥AA1,且MA1=MC.求證:
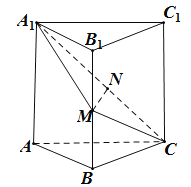
(1)MN![]() 平面ABC;
平面ABC;
(2)平面A1MC⊥平面A1ACC1.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com