【題目】在△ABC中，角A，B，C的對邊分別為 
． （Ⅰ）求cosB的值；
（Ⅱ）若 
，求a和c的值．
【答案】解：（Ⅰ）∵cos 
= 
， ∴sin 
=sin（ 
﹣ ）= ，
∴cosB=1﹣2sin2 = 
．
（Ⅱ）由 
=2可得 accosB=2，又cosB= ，
故ac=6，
由 b2=a2+c2﹣2accosB 可得a2+c2=12，
∴（a﹣c）2=0，
故 a=c，
∴a=c= 
【解析】（1）利用誘導公式求出sin 
的值，從而利用二倍角的余弦公式求得cosB．（2）由兩個向量的數量積的定義求出ac的值，再利用余弦定理求出a和c的值．
【考點精析】認真審題，首先需要了解同角三角函數基本關系的運用(同角三角函數的基本關系：
；
;（3） 倒數關系：
)，還要掌握余弦定理的定義(余弦定理:
;
;
)的相關知識才是答題的關鍵．
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知函數f（x）=|x+a|+|x﹣2|
（1）當a=﹣3時，求不等式f（x）≥3的解集；
（2）若f（x）≤|x﹣4|的解集包含[1，2]，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法錯誤的是（ ）
A. 線性回歸直線
至少經過其樣本數據點中的一個點
B. 在統計學中，獨立性檢驗是檢驗兩個分類變量是否有關系的一種統計方法
C. 在回歸分析中，相關指數
越大，模擬的效果越好
D. 在殘差圖中，殘差分布的帶狀區域的寬度越狹窄，其模擬的效果越好
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某工廠生產不同規格的一種產品，根據檢測標準，其合格產品的質量
與尺寸
之間滿足關系式
（
為大于0的常數），現隨機抽取6件合格產品，測得數據如下：
尺寸 | 38 | 48 | 58 | 68 | 78 | 88 |
質量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
（1）求
關于
的回歸方程；（提示：
與
有線性相關關系）
（2）按照某項指標測定，當產品質量與尺寸的比在區間
內時為優等品，現從抽取的6件合格產品再任選3件，求恰好取得兩件優等品的概率.
參考數據及公式：
，
，
，
對于樣本
（
），其回歸直線
的斜率和截距的最小二乘估計公式分別為：
，
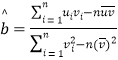查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（1）寫出下列兩組誘導公式：
①關于
與
的誘導公式；
②關于
與的誘導公式.
（2）從上述①②兩組誘導公式中任選一組，用任意角的三角函數定義給出證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
