
設函數 ,
,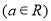 ;
; ,
, .
.
(1)求函數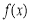 的單調區間;
的單調區間;
(2)當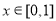 時,求函數
時,求函數 的最大值;
的最大值;
(3)求證:
(1)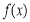 的定義域為
的定義域為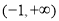 ,
,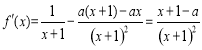 , 1分
, 1分
令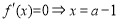 ,
,
ⅰ)當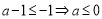 時:
時: 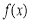 的增區間為
的增區間為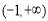 ;
;
ⅱ)當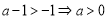 時:
時: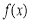 的減區間為
的減區間為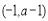 ;
;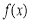 的增區間為
的增區間為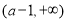 .
.
(2)當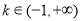 時,
時, 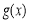 在
在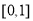 上的最大值為
上的最大值為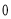 .
.
(3)見解析.
【解析】
試題分析:(1)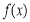 的定義域為
的定義域為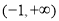 ,
,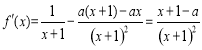 ,
,
分類討論如下:
ⅰ)當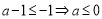 時:
時:
在區間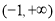 上,
上,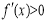 恒成立,故
恒成立,故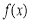 的增區間為
的增區間為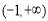 ;
;
ⅱ)當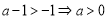 時:
時:
在區間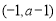 上,
上,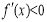 恒成立,故
恒成立,故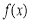 的減區間為
的減區間為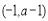 ;
;
在區間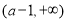 上,
上, 恒成立,故
恒成立,故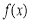 的增區間為
的增區間為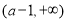 .
.
(2)令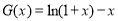 ,
,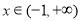 ,則
,則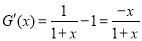 ,利用“表解法”確定函數的最值.
,利用“表解法”確定函數的最值.
表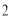 :
:
|
|
|
|
|
|
|
|
| 遞減 | 極小值 | 遞增 |
(3)由(1)可知:當a=1時,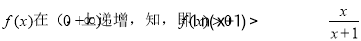
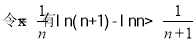 轉化
轉化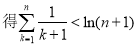
由(2)已證: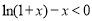
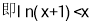
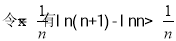
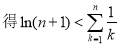 得證.
得證.
試題解析:(1)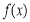 的定義域為
的定義域為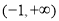 ,
,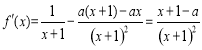 , 1分
, 1分
令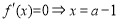 ,
,
ⅰ)當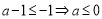 時:
時:
在區間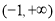 上,
上,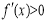 恒成立,故
恒成立,故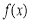 的增區間為
的增區間為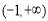 ; 2分
; 2分
ⅱ)當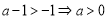 時:
時:
在區間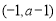 上,
上,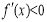 恒成立,故
恒成立,故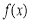 的減區間為
的減區間為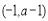 ; 3分
; 3分
在區間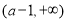 上,
上, 恒成立,故
恒成立,故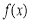 的增區間為
的增區間為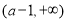 . 4分
. 4分
(2)ⅰ)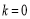 時,
時,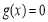 ,所以
,所以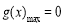 ; 5分
; 5分
ⅱ) 時,易知
時,易知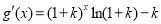 ,于是:
,于是: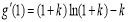 ,
,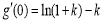 ,
,
由(1)可知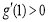 , 下證
, 下證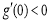 ,即證明不等式
,即證明不等式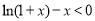 在
在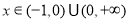 上恒成立.
上恒成立.
(法一)由上可知:不等式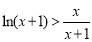 在
在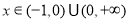 上恒成立,若
上恒成立,若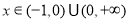 ,則
,則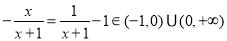 ,故
,故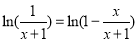
 ,即當
,即當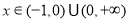 時,
時,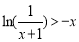 ,從而
,從而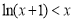 ,故當
,故當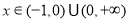 時,
時,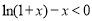 恒成立,即
恒成立,即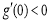 . 7分
. 7分
(法二)令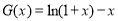 ,
,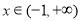 ,則
,則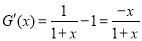 ,列表
,列表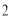 如下:
如下:
表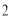 :
:
|
|
|
|
|
|
|
|
| 遞減 | 極小值 | 遞增 |
由表2可知:當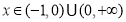 時,
時,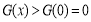 ,
,
故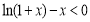 恒成立,即
恒成立,即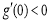 . 7分
. 7分
由于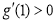 ,且
,且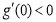 ,故函數
,故函數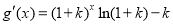 區間
區間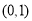 內必存在零點. 8分
內必存在零點. 8分
又當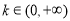 時,
時,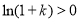 ,指數函數
,指數函數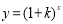 為增函數
為增函數 為增函數,
為增函數,
同理當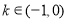 時,
時, ,指數函數
,指數函數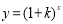 為減函數
為減函數 也為增函數,
也為增函數,
于是,當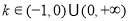 時,
時, 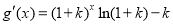 必為增函數,
必為增函數,
從而函數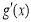 在區間
在區間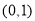 內必存在唯一零點,不妨記為
內必存在唯一零點,不妨記為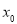 ,則
,則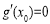 ,
,
易知當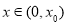 時,
時,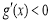 ,此時
,此時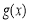 單調遞減;
單調遞減;
當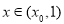 時,
時,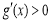 ,此時
,此時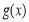 單調遞增,
單調遞增,
又易知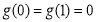 ,故
,故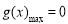 ;
;
綜上,當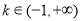 時,
時, 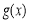 在
在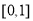 上的最大值為
上的最大值為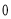 . 10分
. 10分
(3)由(1)可知:當a=1時,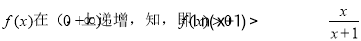
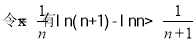
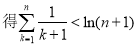 12分
12分
由(2)已證: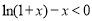
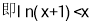
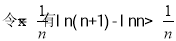
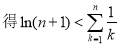
故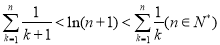 得證 14分
得證 14分
考點:1.應用導數研究函數的單調性;2.應用導數研究函數的單調性、極(最)值,3.應用導數證明不等式4.轉化與化歸思想.


科目:高中數學 來源:2015屆廣東省高三上學期暑假聯考理科數學試卷(解析版) 題型:解答題
設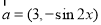 ,
, 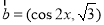 ,
,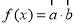
(1)求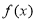 的最小正周期;
的最小正周期;
(2)求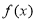 的最大值及取最大值時
的最大值及取最大值時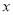 的集合;
的集合;
(3)求滿足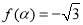 且
且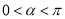 的角
的角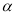 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2015屆廣東省廣州市高三上學期第一次質量檢測理科數學試卷(解析版) 題型:填空題
在平面直角坐標系中,傾斜角為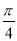 的直線
的直線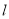 與曲線
與曲線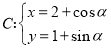 ,(
,(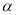 為參數)交于
為參數)交于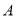 、
、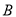 兩點,且
兩點,且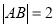 ,以坐標原點
,以坐標原點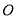 為極點,
為極點, 軸正半軸為極軸建立極坐標系,則直線
軸正半軸為極軸建立極坐標系,則直線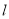 的極坐標方程是________.
的極坐標方程是________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com