【題目】已知四面體
的棱長滿足
，
，現將四面體放入一個主視圖為等邊三角形的圓錐中，使得四面體可以在圓錐中任意轉動，則圓錐側面積的最小值為___________.
【答案】
【解析】
若滿足題意，則四面體的外接球應該內切于圓錐即可.先求得四面體外接球的半徑，再根據該球內切于圓錐，即可求得圓錐側面積的最小值.
若滿足題意，則四面體的外接球應該內切于圓錐即可.
為邏輯清晰，我們將問題主要分為兩步.
第一步：求得四面體
外接球半徑.
記
外心為
，過作平面
的垂線
，
記外接球球心為
，連接
.
則外接球半徑
.下面求解
.
在中，由余弦定理可得
，
則由同角三角函數關系可得
.
故外接圓半徑
.
將
的圖形單獨抽取出來，取
中點為
.如上面由圖所示：
容易知：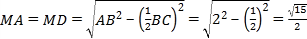
.
在中，因為
，
，
故可得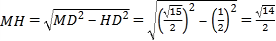
，
.
故可得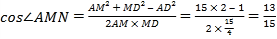
.
又因為
，
解得
.
在
中，容易得
.
故可得
.
在
中，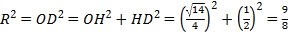
.
故可得四面體外接球半徑
.
第二步：根據外接球半徑和圓錐的關系，求得圓錐的母線和底面圓半徑.
若滿足題意，則該外接球應該內切于圓錐，
作出軸截面的平面圖，其中點為
的中點，如下所示：
該截面圖中
.
由題可知
為等邊三角形，故可得
；
在
中，
，解得
.
故可得圓錐的底面圓半徑為.母線長
.
故可得圓錐的側面積為
.
故答案為：.
科目：高中數學 來源： 題型：
【題目】已知
（1）求
的軌跡
（2）過軌跡
上任意一點
作圓
的切線
，設直線
的斜率分別是
，試問在三個斜率都存在且不為0的條件下，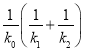 
是否是定值，請說明理由，并加以證明.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某調查機構對全國互聯網行業進行調查統計，得到整個互聯網行業從業者年齡分布餅狀圖、90后從事互聯網行業崗位分布條形圖，則下列結論正確的是（ ）
注：90后指1990年及以后出生，80后指1980-1989年之間出生，80前指1979年及以前出生.
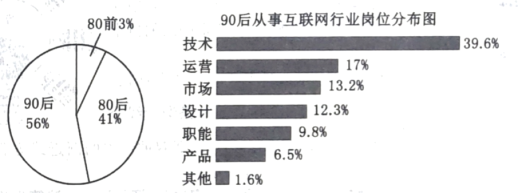
A.互聯網行業從業人員中從事技術和運營崗位的人數占總人數的三成以上
B.互聯網行業中從事技術崗位的人數超過總人數的20%
C.互聯網行業中從事運營崗位的人數90后比80前多
D.互聯網行業中從事技術崗位的人數90后比80后多
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
在區間
上有且僅有2個零點，對于下列4個結論：①在區間
上存在
，滿足
；②
在區間有且僅有1個最大值點；③在區間
上單調遞增；④
的取值范圍是
，其中所有正確結論的編號是( )
A.①③B.①③④C.②③D.①④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲乙兩人同時參加一次數學測試,共有20道選擇題,每題均有4個選項,答對得3分,答錯或不答得0分,甲和乙都解答了所有的試題,經比較,他們只有2道題的選項不同,如果甲最終的得分為54分,那么乙的所有可能的得分值組成的集合為________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
