
【題目】設二次函數f(x)=ax2+bx.
(1)若1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的取值范圍;
(2)當b=1時,若對任意x∈[0,1],-1≤f(x)≤1恒成立,求實數a的取值范圍.
【答案】(1)5≤f(-2)≤10;(2)[-2,0).
【解析】
(1)用![]() 和
和![]() 表示
表示![]() ,再根據不等式的性質求得.
,再根據不等式的性質求得.
(2)對![]() 進行參變分離,根據
進行參變分離,根據 ![]() 和
和![]() 求得.
求得.
解 (1)方法一 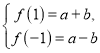
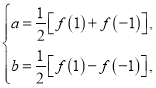
∵f(-2)=4a-2b=3f(-1)+f(1),且1≤f(-1)≤2,2≤f(1)≤4,∴5≤f(-2)≤10.
方法二 設f(-2)=mf(-1)+nf(1),
即4a-2b=m(a-b)+n(a+b)=(m+n)a-(m-n)b,比較兩邊系數:![]()
![]()
∴f(-2)=3f(-1)+f(1),
下同方法一.
(2)當x∈[0,1]時,-1≤f(x)≤1,即-1≤ax2+x≤1,
即當x∈[0,1]時,ax2+x+1≥0且ax2+x-1≤0恒成立;
當x=0時,顯然,ax2+x+1≥0且ax2+x-1≤0均成立;
當x∈(0,1]時,若ax2+x+1≥0恒成立,則a≥-![]() -
-![]() =-(
=-(![]() +
+![]() )2+
)2+![]() ,
,
而-(![]() +
+![]() )2+
)2+![]() 在x∈(0,1]上的最大值為-2,∴a≥-2;
在x∈(0,1]上的最大值為-2,∴a≥-2;
當x∈(0,1]時,ax2+x-1≤0恒成立,則a≤![]() -
-![]() =(
=(![]() -
-![]() )2-
)2-![]() ,
,
而(![]() -
-![]() )2-
)2-![]() 在x∈(0,1]上的最小值為0,∴a≤0,
在x∈(0,1]上的最小值為0,∴a≤0,
∴-2≤a≤0,而a≠0,因此所求a的取值范圍為[-2,0).


 黃岡創優卷系列答案
黃岡創優卷系列答案科目:高中數學 來源: 題型:
【題目】某中學將100名高一新生分成水平相同的甲、乙兩個“平行班”,每班50人.陳老師采用A,B兩種不同的教學方式分別在甲、乙兩個班進行教改實驗.為了了解教學效果,期末考試后,陳老師對甲、乙兩個班級的學生成績進行統計分析,畫出頻率分布直方圖(如下圖).記成績不低于90分者為“成績優秀”.

根據頻率分布直方圖填寫下面2×2列聯表,并判斷能否在犯錯誤的概率不超過0.05的前提下認為:“成績優秀”與教學方式有關.
甲班(A方式) | 乙班(B方式) | 總計 | |
成績優秀 | |||
成績不優秀 | |||
總計 |
附:K2=![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,以
為參數),以坐標原點為極點,以![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點.
兩點.
(1)求直線![]() l的普通方程和曲線
l的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
:![]() ,點
,點![]() 是直線
是直線![]() :
:![]() 上的一動點,過點
上的一動點,過點![]() 作圓M的切線
作圓M的切線![]() 、
、![]() ,切點為
,切點為![]() 、
、![]() .
.
(Ⅰ)當切線PA的長度為![]() 時,求點
時,求點![]() 的坐標;
的坐標;
(Ⅱ)若![]() 的外接圓為圓
的外接圓為圓![]() ,試問:當
,試問:當![]() 運動時,圓
運動時,圓![]() 是否過定點?若存在,求出所有的定點的坐標;若不存在,說明理由;
是否過定點?若存在,求出所有的定點的坐標;若不存在,說明理由;
(Ⅲ)求線段![]() 長度的最小值.
長度的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設每天從甲地去乙地的旅客人數X是服從正態分布N(800,502)的隨機變量.記一天中從甲地去乙地的旅客人數不超過900的概率為p0 .
(1)求p0的值;
(參考數據:若X~N(μ,σ2),有P(μ﹣σ<X≤μ+σ)=0.6826,P(μ﹣2σ<X≤μ+2σ)=0.9544,P(μ﹣3σ<X≤μ+3σ)=0.9974.)
(2)某客運公司用A,B兩種型號的車輛承擔甲、乙兩地間的長途客運業務,每車每天往返一次,A,B兩種車輛的載客量分別為36人和60人,從甲地去乙地的營運成本分別為1600元/輛和2400元/輛.公司擬組建一個不超過21輛車的客運車隊,并要求B型車不多于A型車7輛.若每天要以不小于p0的概率運完從甲地去乙地的旅客,且使公司從甲地去乙地的營運成本最小,那么應配備A型車、B型車各多少輛?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在奧運知識有獎問答競賽中,甲、乙、丙三人同時回答一道有關奧運知識的問題,已知甲答對這道題的概率是![]() ,甲、乙兩人都回答錯誤的概率是
,甲、乙兩人都回答錯誤的概率是![]() ,乙、丙兩人都回答正確的概率是
,乙、丙兩人都回答正確的概率是![]() .設每人回答問題正確與否相互獨立的.
.設每人回答問題正確與否相互獨立的.
(Ⅰ)求乙答對這道題的概率;
(Ⅱ)求甲、乙、丙三人中,至少有一人答對這道題的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x﹣alnx(a∈R)
(1)當a=2時,求曲線y=f(x)在點A(1,f(1))處的切線方程;
(2)求函數f(x)的極值.
查看答案和解析>>