
 贏在課堂名師課時(shí)計(jì)劃系列答案
贏在課堂名師課時(shí)計(jì)劃系列答案 天天向上課時(shí)同步訓(xùn)練系列答案
天天向上課時(shí)同步訓(xùn)練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
在數(shù)列 中,已知
中,已知 ,
, ,
, (
( ,
, ).
).
(1)當(dāng) ,
,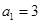 時(shí),分別求
時(shí),分別求 的值,判斷
的值,判斷 是否為定值,并給出證明;
是否為定值,并給出證明;
(2)求出所有的正整數(shù) ,使得
,使得 為完全平方數(shù).
為完全平方數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
將正整數(shù)12分解成兩個(gè)正整數(shù)的乘積有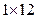 ,
, ,
,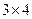 三種,其中
三種,其中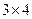 是這三種分解中,兩數(shù)差的絕對值最小的,我們稱
是這三種分解中,兩數(shù)差的絕對值最小的,我們稱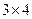 為12的最佳分解.當(dāng)
為12的最佳分解.當(dāng)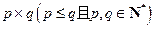 是正整數(shù)
是正整數(shù)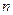 的最佳分解時(shí),我們規(guī)定函數(shù)
的最佳分解時(shí),我們規(guī)定函數(shù)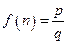 ,例如
,例如 .關(guān)于函數(shù)
.關(guān)于函數(shù)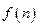 有下列敘述:①
有下列敘述:①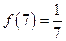 ,②
,②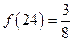 ,③
,③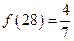 ,④
,④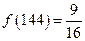 .其中正確的序號為 (填入所有正確的序號).
.其中正確的序號為 (填入所有正確的序號).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
觀察下列等式: 根據(jù)上述規(guī)律,第五個(gè)等式為______________________________________
根據(jù)上述規(guī)律,第五個(gè)等式為______________________________________
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
在解決問題:“證明數(shù)集 沒有最小數(shù)”時(shí),可用反證法證明.
沒有最小數(shù)”時(shí),可用反證法證明.
假設(shè) 是
是 中的最小數(shù),則取
中的最小數(shù),則取 ,可得:
,可得: ,與假設(shè)中“
,與假設(shè)中“ 是
是 中的最小數(shù)”矛盾!那么對于問題:“證明數(shù)集
中的最小數(shù)”矛盾!那么對于問題:“證明數(shù)集 沒有最大數(shù)”,也可以用反證法證明.我們可以假設(shè)
沒有最大數(shù)”,也可以用反證法證明.我們可以假設(shè) 是
是 中的最大數(shù),則可以找到
中的最大數(shù),則可以找到 ▲ (用
▲ (用 ,
, 表示),由此可知
表示),由此可知 ,
, ,這與假設(shè)矛盾!所以數(shù)集
,這與假設(shè)矛盾!所以數(shù)集 沒有最大數(shù).
沒有最大數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
在平面幾何里,有:“若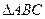 的三邊長分別為
的三邊長分別為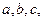 內(nèi)切圓半徑為
內(nèi)切圓半徑為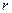 ,則三角形面積為
,則三角形面積為 ”,拓展到空間,類比上述結(jié)論,“若四面體
”,拓展到空間,類比上述結(jié)論,“若四面體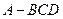 的四個(gè)面的面積分別為
的四個(gè)面的面積分別為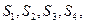 內(nèi)切球的半徑為
內(nèi)切球的半徑為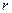 ,則四面體的體積為 ”
,則四面體的體積為 ”
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
“無理數(shù)是無限小數(shù),而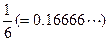 是無限小數(shù),所以
是無限小數(shù),所以 是無理數(shù)。”
是無理數(shù)。”
這個(gè)推理是 _推理(在“歸納”、“類比”、“演繹”中選擇填空)
查看答案和解析>>