
【題目】已知函數![]() .
.
(1)當![]() 時,若函數
時,若函數![]() 在
在![]() ,
,![]() (
(![]() )處導數相等,證明:
)處導數相等,證明:![]() ;
;
(2)是否存在![]() ,使直線
,使直線![]() 是曲線
是曲線![]() 的切線,也是曲線
的切線,也是曲線![]() 的切線,而且這樣的直線
的切線,而且這樣的直線![]() 是唯一的,如果存在,求出直線
是唯一的,如果存在,求出直線![]() 方程,如果不存在,請說明理由.
方程,如果不存在,請說明理由.
【答案】(1)見解析(2)存在,![]()
【解析】
(1)求導![]() ,則
,則![]() ,化簡得到
,化簡得到![]() ,再利用均值不等式到答案.
,再利用均值不等式到答案.
(2)先設切點求切線方程,再根據切線重合得關于一個切點橫坐標的函數,利用導數研究函數只有一個零點的情況,即得答案.
(1)當![]() 時,
時,![]() ,所以
,所以![]() ,
,
由題意,得![]() ,因為
,因為![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() .
.
(2)曲線![]() 在點
在點![]() 處的切線方程為:
處的切線方程為:
![]() ,
,
函數![]() 在點
在點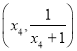 處的切線方程
處的切線方程 ,
,
要存在直線![]() ,使
,使![]() 是曲線
是曲線![]() 的切線,也是曲線
的切線,也是曲線![]() 的切線,
的切線,
只需在![]() 處使
處使![]() 與
與![]() 重合,
重合,
所以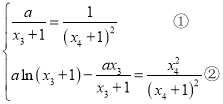
由①得![]() 代入②整理得
代入②整理得![]() ,
,
設![]() ,
,
則![]() ,
,
當![]() 時,
時,![]() ,
,![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,
,![]() 單調遞增,
單調遞增,
則![]() ,設
,設![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,
,![]() 單調遞增;
單調遞增;
當![]() 時,
時,![]() ,
,![]() 單調遞減.
單調遞減.
所以![]() .
.
(ⅰ)當![]() 時,
時,![]() ,所以
,所以![]() ,
,
此時![]() ,所以方程
,所以方程![]() 有唯一解
有唯一解![]() ,
,
即![]() ,此時切線方程為
,此時切線方程為![]() ;
;
(ⅱ)當![]() 且
且![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,則
,則![]() ,
,
故![]() 函數單調遞增,當
函數單調遞增,當![]() 時,函數單調遞減,故
時,函數單調遞減,故![]() ,
,
故![]() ,同理可證
,同理可證![]() ,
,![]() 成立.
成立.
因為![]() ,則
,則![]()
![]()
![]()
![]() .
.
又由當![]() 時,
時,![]() ,可得
,可得![]() ,
,
則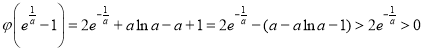 ,
,
所以函數![]() 有兩個零點,
有兩個零點,
即方程![]() 有兩個根
有兩個根![]() ,
,![]() ,
,
即![]() ,此時
,此時![]() ,
,![]() ,則
,則![]() ,
,
所以![]() ,
,
因為![]() ,
,![]() ,所以
,所以![]() ,所以直線
,所以直線![]() 不唯一.
不唯一.
綜上所述,存在![]() ,使
,使![]() 是曲線
是曲線![]() 的切線,也是曲線
的切線,也是曲線![]() 的切線,而且這樣的直線
的切線,而且這樣的直線![]() 是唯一的.
是唯一的.


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案科目:高中數學 來源: 題型:
【題目】△ABC中,角A,B,C的對邊分別為a,b,c,且(a+b﹣c)(sinA+sinB+sinC)=bsinA.
(1)求C;
(2)若a=2,c=5,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為正方形,
為正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 為線段
為線段![]() 的中點.
的中點.
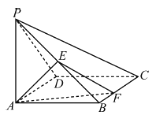
(1)若![]() 為線段
為線段![]() 上的動點,證明:平面
上的動點,證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 為線段
為線段![]() ,
,![]() ,
,![]() 上的動點(不含
上的動點(不含![]() ,
,![]() ),
),![]() ,三棱錐
,三棱錐![]() 的體積是否存在最大值?如果存在,求出最大值;如果不存在,請說明理由.
的體積是否存在最大值?如果存在,求出最大值;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 上任意一點
上任意一點![]() 滿足
滿足![]() ,直線
,直線![]() 的方程為
的方程為![]() ,且與曲線
,且與曲線![]() 交于不同兩點
交于不同兩點![]() ,
,![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)設點![]() ,直線
,直線![]() 與
與![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,且
,且![]() ,判斷直線
,判斷直線![]() 是否過定點?若過定點,求該定點的坐標.
是否過定點?若過定點,求該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直線l的參數方程為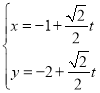 (t為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρsin2θ=4acosθ,直線l與曲線C交于不同的兩點M,N.
(t為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρsin2θ=4acosθ,直線l與曲線C交于不同的兩點M,N.
(1)求實數a的取值范圍;
(2)已知a>0,設點P(﹣1,﹣2),若|PM|,|MN|,|PN|成等比數列,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】1772年德國的天文學家波得發現了求太陽的行星距離的法則,記地球距離太陽的平均距離為10,可以算得當時已知的六大行星距離太陽的平均距離如下表:
星名 | 水星 | 金星 | 地球 | 火星 | 木星 | 土星 |
與太陽的距離 | 4 | 7 | 10 | 16 | 52 | 100 |
除水星外,其余各星與太陽的距離都滿足波得定則(某一數列規律),當時德國數學家高斯根據此定則推算,火星和木星之間距離太陽28還有一顆大行星,1801年,意大利天文學家皮亞齊經過觀測,果然找到了火星和木星之間距離太陽28的谷神星以及它所在的小行星帶,請你根據這個定則,估算從水星開始由近到遠算,第10個行星與太陽的平均距離大約是( )
A.388B.772C.1540D.3076
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com