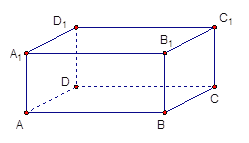
【題目】長方體
中，
（1）求直線
與
所成角；
（2）求直線與平面
所成角的正弦.
【答案】（1）直線
所成角為90°；（2）
。
【解析】
試題（1）建立空間直角坐標系，求出直線AD1與B1D的方向向量，利用向量的夾角公式，即可求直線AD1與B1D所成角；
（2）求出平面B1BDD1的法向量，利用向量的夾角公式，即可求直線AD1與平面B1BDD1所成角的正弦．
解：（1）建立如圖所示的直角坐標系，則A（0，0，0），D1（1，0，1），B1（0，2，1），D（1，0，0）．
∴
，
∴cos
=
=0，
∴
=90°，
∴直線AD1與B1D所成角為90°；
（2）設平面B1BDD1的法向量
=（x，y，z），則
∵
，
=（﹣1，2，0），
∴
，
∴可取=（2，1，0），
∴直線AD1與平面B1BDD1所成角的正弦為
=
．
科目：高中數學 來源： 題型：
【題目】已知數列
中，已知
，
對任意
都成立，數列的前n項和為
．
（1）若是等差數列，求k的值；
（2）若
，
，求；
（3）是否存在實數k，使數列是公比不為1的等比數列，且任意相鄰三項
，
，
按某順序排列后成等差數列？若存在，求出所有k的值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
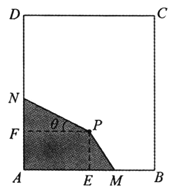
【題目】（題文）如圖，長方形材料
中，已知
，
.點
為材料內部一點，
于
，
于
，且
，
. 現要在長方形材料中裁剪出四邊形材料
，滿足
，點
、
分別在邊
，
上.
（1）設
，試將四邊形材料的面積表示為
的函數，并指明的取值范圍；
（2）試確定點在上的位置，使得四邊形材料的面積
最小，并求出其最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是一矩形濱河公園
，其中
長為
百米，
長為
百米，的中點
為便民服務中心.根據居民實際需求，現規劃建造三條步行通道
、
及
，要求點
、
分別在公園邊界
、上，且
.
（1）設
.①求步道總長度
關于
的函數解析式
；②求函數的定義域.
（2）為使建造成本最低，需步行通道總長最短，試求步行通道總長度的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數
，其中
.
（1）求函數
的單調區間；
（2）已知當
（其中
是自然對數）時，在
上至少存在一點
，使
成立，求
的取值范圍；
（3）求證：當
時，對任意
， 
，有
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2017年“雙節”期間，高速公路車輛較多．某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查，將他們在某段高速公路的車速
分成六段： 
， 
， 
， 
， 
， 
后得到如圖的頻率分布直方圖．
（1）調查公司在采樣中，用到的是什么抽樣方法？
（2）求這40輛小型車輛車速的眾數、中位數及平均數的估計值；
（3）若從車速在
的車輛中任抽取2輛，求車速在的車輛至少有一輛的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
是不重合直線，
是不重合平面，則下列命題
①若
，則
∥
②若
∥
∥，則∥
③若∥、
∥，則∥
④若
，則
∥
⑤若
，則∥
為假命題的是
A. ①②③ B. ①②⑤ C. ③④⑤ D. ①②④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，平面中兩條直線
和
相交于點O，對于平面上任意一點M，若p，q分別是M到直線和的距離，則稱有序非負實數對
是點M的“距離坐標”.下列四個命題中正確命題為( )
A.若
，則“距離坐標”為
的點有且僅有1個
B.若
，且
，則“距離坐標”為的點有且僅有2個
C.若
，則“距離坐標”為的點有且僅有4個
D.若
，則點M在一條過點O的直線上
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
