
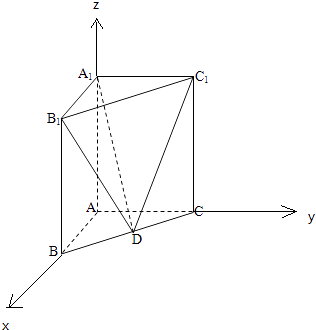
【題目】如圖,在直三棱柱ABC﹣A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3.D是線段BC的中點. 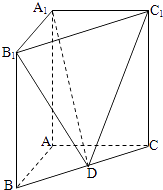
(1)求直線DB1與平面A1C1D所成角的正弦值;
(2)求二面角B1﹣A1D﹣C1的大小的余弦值.
【答案】
(1)解:因為在直三棱柱ABC﹣A1B1C1中,AB⊥AC,
所以分別以AB、AC、AA1所在的直線為x軸、y軸、z軸,建立空間直角坐標系,
則A(0,0,0),B(2,0,0),C(0,4,0),A1(0,0,3),B1(2,0,3),C1(0,4,3),
因為D是BC的中點,所以D(1,2,0),
因為 ![]() ,設平面A1C1D的法向量
,設平面A1C1D的法向量 ![]() ,
,
則 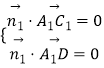 ,即
,即 ![]() ,取
,取 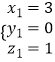 ,
,
所以平面A1C1D的法向量 ![]() ,而
,而 ![]() ,
,
所以 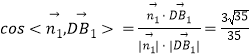 ,
,
所以直線DB1與平面A1C1D所成角的正弦值為 ![]()
(2)解: ![]() ,
, ![]() ,
,
設平面B1A1D的法向量 ![]() ,
,
則 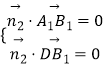 ,即
,即 ![]() ,
,
取 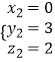 ,平面B1A1D的法向量
,平面B1A1D的法向量 ![]() ,
,
所以 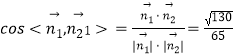 ,
,
二面角B1﹣A1D﹣C1的大小的余弦值 ![]() .
.
【解析】(1)分別以AB、AC、AA1所在的直線為x軸、y軸、z軸,建立空間直角坐標系,利用向量法能求出直線DB1與平面A1C1D所成角的正弦值.(2)求出平面B1A1D的法向量和平面B1A1D的法向量,利用向量法能求出二面角B1﹣A1D﹣C1的大小的余弦值.
【考點精析】根據題目的已知條件,利用空間角的異面直線所成的角的相關知識可以得到問題的答案,需要掌握已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則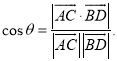 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某高校共有學生15 000人,其中男生10 500人,女生4500人.為調查該校學生每周平均體育運動時間的情況,采用分層抽樣的方法,收集300位學生每周平均體育運動時間(單位:h)的樣本數據.

(1)應收集多少位女生的樣本數據?
(2)根據這300個樣本數據,得到學生每周平均體育運動時間的頻率分布直方圖(如圖所示),其中樣本數據的分組區間為[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].估計該校學生每周平均體育運動時間超過4 h的概率.
(3)在樣本數據中,有60位女生的每周平均體育運動時間超過4 h,請完成下面的2×2列聯表,并判斷是否有95%的把握認為“該校學生的每周平均體育運動時間與性別有關”?
男生 | 女生 | 總計 | |
每周平均體育運動時間不超過4h | |||
每周平均體育運動時間超過4h | |||
總計 |
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】研究變量![]() ,
,![]() 得到一組樣本數據,進行回歸分析,有以下結論
得到一組樣本數據,進行回歸分析,有以下結論
①殘差平方和越小的模型,擬合的效果越好;
②用相關指數![]() 來刻畫回歸效果,
來刻畫回歸效果,![]() 越小說明擬合效果越好;
越小說明擬合效果越好;
③在回歸直線方程![]() 中,當解釋變量
中,當解釋變量![]() 每增加1個單位時,預報變量
每增加1個單位時,預報變量![]() 平均增加0.2個單位
平均增加0.2個單位
④若變量![]() 和
和![]() 之間的相關系數為
之間的相關系數為![]() ,則變量
,則變量![]() 和
和![]() 之間的負相關很強,以上正確說法的個數是( )
之間的負相關很強,以上正確說法的個數是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知非空集合M滿足M{0,1,2,…,n}(n≥2,n∈N+).若存在非負整數k(k≤n),使得當a∈M時,均有2k﹣a∈M,則稱集合M具有性質P.設具有性質P的集合M的個數為f(n).
(1)求f(2)的值;
(2)求f(n)的表達式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (a>b>0)的一個頂點為A(2,0),離心率為
(a>b>0)的一個頂點為A(2,0),離心率為![]() .直線y=k(x-1)與橢圓C交于不同的兩點M,N.
.直線y=k(x-1)與橢圓C交于不同的兩點M,N.
(1)求橢圓C的方程;
(2)當△AMN的面積為![]() 時,求k的值.
時,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3-3mx+n(m>0)的極大值為6,極小值為2.
(1)求實數m,n的值;
(2)求f(x)在區間[0,3]上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若正整數N除以正整數m后的余數為n,則記為N≡n(mod m),例如10≡4(mod 6).下面程序框圖的算法源于我國古代聞名中外的(中國剩余定理),執行該程序框圖,則輸出的n等于( ) 
A.17
B.16
C.15
D.13
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,底面ABCD為菱形,∠BAD=60°,Q是AD的中點. 
(1)若PA=PD,求證:平面PQB⊥平面PAD;
(2)若平面APD⊥平面ABCD,且PA=PD=AD=2,在線段PC上是否存在點M,使二面角M﹣BQ﹣C的大小為60°.若存在,試確定點M的位置,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com