
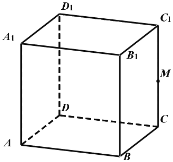
【題目】如圖,![]() 點在正方體
點在正方體![]() 的棱
的棱![]() 上(不含端點),給出下列五個命題:
上(不含端點),給出下列五個命題:
①過![]() 點有且只有一條直線與直線
點有且只有一條直線與直線![]() ,
,![]() 都是異面直線;
都是異面直線;
②過![]() 點有且只有一條直線與直線
點有且只有一條直線與直線![]() ,
,![]() 都相交;
都相交;
③過![]() 點有且只有一條直線與直線
點有且只有一條直線與直線![]() ,
,![]() 都垂直;
都垂直;
④過![]() 點有無數個平面與直線
點有無數個平面與直線![]() ,
,![]() 都相交;
都相交;
⑤過![]() 點有無數個平面與直線
點有無數個平面與直線![]() ,
,![]() 都平行;
都平行;
其中真命題是____.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知數列![]() 是各項均不為0的等差數列,公差為
是各項均不為0的等差數列,公差為![]() ,
,![]() 為其前
為其前![]() 項和,且滿足
項和,且滿足![]() .數列
.數列![]() 滿足
滿足![]() ,
,![]() 為數列
為數列![]() 的前
的前![]() 項和.
項和.
(1)求![]() ;
;
(2)求![]() ;
;
(3)若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“干支紀年法”是中國歷法上自古以來使用的紀年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被稱為“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。“天干”以“甲”字開始,“地支”以“子”字開始,兩者按干支順序相配,組成了干支紀年法,其相配順序為:甲子、乙丑、丙寅…癸酉,甲戌、乙亥、丙子…癸未,甲申、乙酉、丙戌…癸巳,…,共得到60個組合,稱六十甲子,周而復始,無窮無盡。2019年是“干支紀年法”中的己亥年,那么2026年是“干支紀年法”中的
A. 甲辰年B. 乙巳年C. 丙午年D. 丁未年
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AD∥BC,![]() ADC=
ADC=![]() PAB=90°,BC=CD=
PAB=90°,BC=CD=![]() AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.
AD.E為棱AD的中點,異面直線PA與CD所成的角為90°.

(I)在平面PAB內找一點M,使得直線CM∥平面PBE,并說明理由;
(II)若二面角P-CD-A的大小為45°,求直線PA與平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其導函數設為
,其導函數設為![]() .
.
(Ⅰ)求函數![]() 的單調區間;
的單調區間;
(Ⅱ)若函數![]() 有兩個極值點
有兩個極值點![]() ,
,![]() ,試用
,試用![]() 表示
表示![]() ;
;
(Ⅲ)在(Ⅱ)的條件下,若![]() 的極值點恰為
的極值點恰為![]() 的零點,試求
的零點,試求![]() ,
,![]() 這兩個函數的所有極值之和的取值范圍.
這兩個函數的所有極值之和的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】本市攝影協會準備在2019年10月舉辦主題為“慶祖國70華誕——我們都是追夢人”攝影圖片展.通過平常人的鏡頭記錄國強民富的幸福生活,向祖國母親的生日獻禮.攝影協會收到了來自社會各界的大量作品,打算從眾多照片中選取100張照片展出,其參賽者年齡集中在![]() 之間,根據統計結果,做出頻率分布直方圖如圖:
之間,根據統計結果,做出頻率分布直方圖如圖:
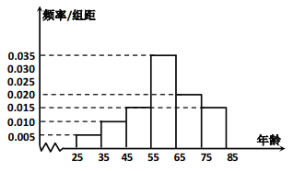
(1)根據頻率分布直方圖,求這100位攝影者年齡的樣本平均數![]() 和中位數
和中位數![]() (同一組數據用該區間的中點值作代表);
(同一組數據用該區間的中點值作代表);
(2)為了展示不同年齡作者眼中的祖國形象,攝影協會按照分層抽樣的方法,計劃從這100件照片中評出20個最佳作品,并邀請作者參加“講述照片背后的故事”座談會.
①在答題卡上的統計表中填出每組應抽取的人數;
年齡 |
|
|
|
|
|
|
人數 |
②若從較年輕的前三組作者中選出2人把這些圖片和故事整理成冊,求這2人至少有一人的年齡在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司新上一條生產線,為保證新的生產線正常工作,需對該生產線進行檢測,現從該生產線上隨機抽取100件產品,測量產品數據,用統計方法得到樣本的平均數![]() ,標準差
,標準差![]() ,繪制如圖所示的頻率分布直方圖,以頻率值作為概率估值。
,繪制如圖所示的頻率分布直方圖,以頻率值作為概率估值。
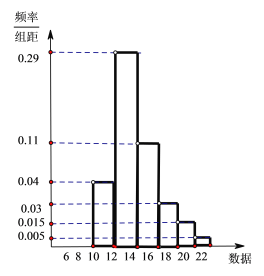
(1)從該生產線加工的產品中任意抽取一件,記其數據為![]() ,依據以下不等式評判(
,依據以下不等式評判(![]() 表示對應事件的概率)
表示對應事件的概率)
①![]()
②![]()
③![]()
評判規則為:若至少滿足以上兩個不等式,則生產狀況為優,無需檢修;否則需檢修生產線,試判斷該生產線是否需要檢修;
(2)將數據不在![]() 內的產品視為次品,從該生產線加工的產品中任意抽取2件,次品數記為
內的產品視為次品,從該生產線加工的產品中任意抽取2件,次品數記為![]() ,求
,求![]() 的分布列與數學期望
的分布列與數學期望![]() 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知![]() 為等邊三角形,
為等邊三角形,![]() 為等腰直角三角形,
為等腰直角三角形,![]() .平面
.平面![]() 平面ABD,點E與點D在平面ABC的同側,且
平面ABD,點E與點D在平面ABC的同側,且![]() ,
,![]() .點F為AD中點,連接EF.
.點F為AD中點,連接EF.
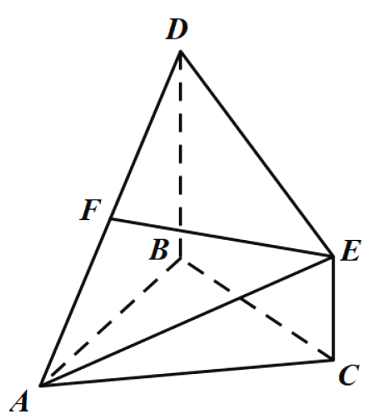
(1)求證:![]() 平面ABC;
平面ABC;
(2)求證:平面![]() 平面ABD.
平面ABD.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com