【題目】已知△ABC的角A、B、C所對(duì)的邊分別是a、b、c，設(shè)向量 
， 
， 
．
（1）若 
∥ 
，求證：△ABC為等腰三角形；
（2）若 ⊥ ，邊長(zhǎng)c=2，角C= 
，求△ABC的面積．
【答案】
（1）證明：∵m∥n
∴asinA=bsinB
即a 
=b 
．其中R為△ABC外接圓半徑．
∴a=b
∴△ABC為等腰三角形
（2）解：由題意，mp=0
∴a（b﹣2）+b（a﹣2）=0
∴a+b=ab
由余弦定理4=a2+b2﹣2abcos 
∴4=a2+b2﹣ab=（a+b）2﹣3ab
∴（ab）2﹣3ab﹣4=0
∴ab=4或ab=﹣1（舍去）
∴S△ABC= 
absinC
= ×4×sin = 
【解析】（1）利用向量平行的條件，寫出向量平行坐標(biāo)形式的條件，得到關(guān)于三角形的邊和角之間的關(guān)系，利用余弦定理變形得到三角形是等腰三角形．（2）利用向量垂直數(shù)量積為零，寫出三角形邊之間的關(guān)系，結(jié)合余弦定理得到求三角形面積所需的兩邊的乘積的值，求出三角形的面積．
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在平面直角坐標(biāo)系
中，拋物線
的頂點(diǎn)是原點(diǎn)，以
軸為對(duì)稱軸，且經(jīng)過點(diǎn)
.
（Ⅰ）求拋物線
的方程；
（Ⅱ）設(shè)點(diǎn)
， 
在拋物線
上，直線
， 
分別與
軸交于點(diǎn)
， 
， 
.求直線
的斜率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】當(dāng)
，則稱點(diǎn)
為平面上單調(diào)格點(diǎn)：設(shè)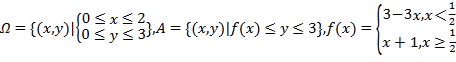
求從區(qū)域
中任取一點(diǎn)
，而該點(diǎn)落在區(qū)域
上的概率；
求從區(qū)域
中的所有格點(diǎn)中任取一點(diǎn)
，而該點(diǎn)是區(qū)域
上的格點(diǎn)的概率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】寶寶的健康成長(zhǎng)是媽媽們最關(guān)心的問題，父母親為嬰兒選擇什么品牌的奶粉一直以來都是育嬰中的一個(gè)重要話題，為了解過程奶粉的知名度和消費(fèi)者的信任度，某調(diào)查小組特別調(diào)查記錄了某大型連鎖超市2015年與2016年這兩年銷售量前5名的五個(gè)品牌奶粉的銷量（單位：罐），繪制如下的管狀圖：
（1）根據(jù)給出的這兩年銷量的管狀圖，對(duì)該超市這兩年品牌奶粉銷量的前五強(qiáng)進(jìn)行排名；
（2）分別計(jì)算這5個(gè)品牌奶粉2016年所占總銷量（僅指這5個(gè)品牌奶粉的總銷量）的百分比（百分?jǐn)?shù)精確到各位），并將數(shù)據(jù)填入如下餅狀圖中的括號(hào)內(nèi)；
（3）已知該超市2014年飛鶴奶粉的銷量為
（單位：罐），試以
這3年的銷量得出銷量
關(guān)于
年份的線性回歸方程，并據(jù)此預(yù)測(cè)2017年該超市飛鶴奶粉的銷量.
相關(guān)公式： 
.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知經(jīng)過原點(diǎn)的直線與橢圓
交于
兩點(diǎn)，點(diǎn)
為橢圓上不同于
的一點(diǎn)，直線
的斜率均存在，且直線
的斜率之積為
.
（1）求橢圓
的離心率；
（2）若
，設(shè)
分別為橢圓的左、右焦點(diǎn)，斜率為
的直線
經(jīng)過橢圓的右焦點(diǎn)，且與橢圓交于
兩點(diǎn)，若點(diǎn)
在以
為直徑的圓內(nèi)部，求
的取值范圍.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖,直線
與圓 
且與橢圓
相交于
兩點(diǎn).
(1)若直線
恰好經(jīng)過橢圓的左頂點(diǎn),求弦長(zhǎng)
(2)設(shè)直線
的斜率分別為
,判斷
是否為定值,并說明理由
(3)求
，面積的最小值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】我國(guó)是世界上嚴(yán)重缺水的國(guó)家，某市政府為了鼓勵(lì)居民節(jié)約用水，計(jì)劃調(diào)整居民生活用水收費(fèi)方案，擬確定一個(gè)合理的月用水量標(biāo)準(zhǔn)
（噸），一位居民的月用水量不超過
的部分按平價(jià)收費(fèi)，超過
的部分按議價(jià)收費(fèi)，為了了解居民用水情況，通過抽樣，獲得了某年100位居民每人的月均用水量（單位：噸），將數(shù)據(jù)按照
， 
，…， 
分成9組，制成了如圖所示的頻率分布直方圖.
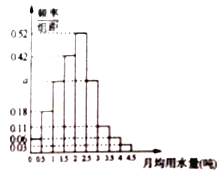
（1）求直方圖中
的值；
（2）若將頻率視為概率，從該城市居民中隨機(jī)抽取3人，記這3人中月均用水量不低于3噸的人數(shù)為
，求
的分布列與數(shù)學(xué)期望.
（3）若該市政府希望使85%的居民每月的用水量不超過標(biāo)準(zhǔn)
（噸），估計(jì)
的值（精確到0.01），并說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
， 
，其中
， 
為常數(shù)．
（1）若
是函數(shù)
的一個(gè)極值點(diǎn)，求曲線
在點(diǎn)
處的切線方程；
（2）若函數(shù)
有2個(gè)零點(diǎn)， 
有6個(gè)零點(diǎn)，求
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)Sn是數(shù)列{an}的前n項(xiàng)和，且2an+Sn=An2+Bn+C．
（1）當(dāng)A=B=0，C=1時(shí)，求an；
（2）若數(shù)列{an}為等差數(shù)列，且A=1，C=﹣2． ①設(shè)bn=2nan ， 求數(shù)列{bn}的前n項(xiàng)和；
②設(shè)cn= 
，若不等式cn≥ 
對(duì)任意n∈N*恒成立，求實(shí)數(shù)m的取值范圍．
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話：027-86699610 舉報(bào)郵箱：58377363@163.com