
(本小題滿分14分)已知集合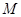 是滿足下列性質的函數
是滿足下列性質的函數 的全體:在定義域內存在
的全體:在定義域內存在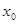 ,使得
,使得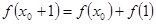 成立。
成立。
(Ⅰ)函數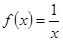 是否屬于集合
是否屬于集合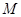 ?說明理由;
?說明理由;
(Ⅱ)設函數 ,求
,求 的取值范圍;
的取值范圍;
(Ⅲ)設函數 圖象與函數
圖象與函數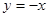 的圖象有交點,
的圖象有交點,
證明:函數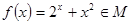 。
。
(Ⅰ)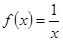
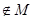 。(Ⅱ)
。(Ⅱ)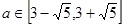 。 (Ⅲ)見解析。
。 (Ⅲ)見解析。
解析試題分析:(1)根據題意,只要sin(x0+1)=sinx0+sin1成立即可,由解析式列出方程,再由特殊角的正弦值進行證明;
(2)把解析式代入f(x+1)=f(x)+f(1),列出對應的方程,再由一元二次方程有解的條件求出k的范圍,注意二次系數是否為零;
(3)根據定義只要證明f(x+1)=f(x)+f(1)有解,把解析式代入列出方程,轉化為對應的函數,利用函數的零點存在性判定理進行判斷..
(Ⅰ)若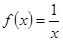
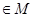 ,在定義域內存在
,在定義域內存在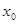 ,則
,則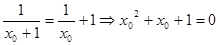 , ∵方程
, ∵方程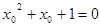 無解,∴
無解,∴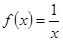
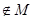 。
。
(Ⅱ)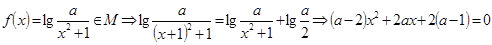 ,
,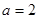 時,
時,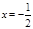 ;
;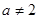 時,由
時,由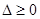 ,得
,得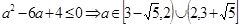 。
。
∴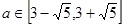 。
。
(Ⅲ)∵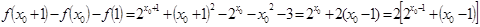 ,
,
又∵函數 圖象與函數
圖象與函數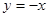 的圖象有交點,設交點的橫坐標為
的圖象有交點,設交點的橫坐標為 ,
,
則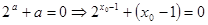 ,其中
,其中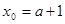 。
。
∴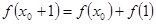 ,即
,即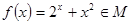 。
。
考點:對數函數圖像與性質的綜合應用.
點評:本題屬于新定義,新情景的問題,主要利用新定義進行運算,考查了對數函數、正弦函數和指數函數的性質,函數的零點存在性判定理的應用,綜合性強、難度大.


科目:高中數學 來源: 題型:解答題
(本題14分)如圖,一水渠的橫斷面是拋物線形,O是拋物線的頂點,口寬EF=4米,高3米,建立適當的直角坐標系,(1)求拋物線方程.(2)若將水渠橫斷面改造成等腰梯形ABCD,要求高度不變,只挖土,不填土,求梯形ABCD的下底AB多大時,所挖的土最少? 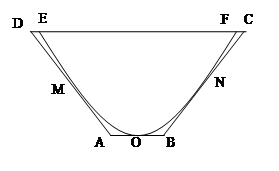
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分15分)設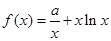 ,
,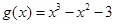 .
.
(1)當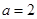 時,求曲線
時,求曲線 在
在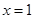 處的切線的斜率;
處的切線的斜率;
(2)如果存在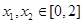 ,使得
,使得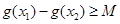 成立,求滿足上述條件的最大整數
成立,求滿足上述條件的最大整數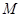 ;
;
(3)如果對于任意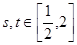 ,都有
,都有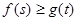 成立,求實數
成立,求實數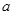 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分14分)
某市郊區一村民小組有100戶農民,且都從事蔬菜種植.據調查,平均每戶的年收入為3萬元.為了調整產業結構,郊區政府決定動員該村部分農民從事蔬菜加工.據預測,若能動員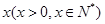 戶農民從事蔬菜加工,則剩下的繼續從事蔬菜種植的農民平均每戶的年收入有望提高
戶農民從事蔬菜加工,則剩下的繼續從事蔬菜種植的農民平均每戶的年收入有望提高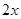 %,而從事蔬菜加工的農民平均每戶的年收入將為
%,而從事蔬菜加工的農民平均每戶的年收入將為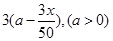 萬元.
萬元.
(1)在動員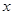 戶農民從事蔬菜加工后,要使從事蔬菜種植的農民的總年收入不低于動員前從事蔬菜種植的農民的總年收入,求
戶農民從事蔬菜加工后,要使從事蔬菜種植的農民的總年收入不低于動員前從事蔬菜種植的農民的總年收入,求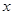 的取值范圍;
的取值范圍;
(2)在(1)的條件下,要使這100戶農民中從事蔬菜加工的農民的總年收入始終不高于從事蔬菜種植的農民的總年收入,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
14分)某出版社新出版一本高考復習用書,該書的成本為5元/本,經銷過程中每本書需付給代理商m元(1≤m≤3)的勞務費,且出版的書可全部銷售完. 經出版社研究決定,新書投放市場后定價為 元/本(9≤
元/本(9≤ ≤11),預計一年的銷售量為
≤11),預計一年的銷售量為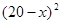 萬本.
萬本.
(1)求該出版社一年的利潤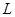 (萬元)與每本書的定價
(萬元)與每本書的定價 的函數關系式;
的函數關系式;
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題12分)某公司生產一種產品每年需投入固定成本為0.5萬元,此外每生產100件這種產品還需要增加投入0.25萬元.經預測知,當售出這種產品 百件時,若
百件時,若 ,則銷售所得的收入為
,則銷售所得的收入為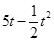 萬元:若
萬元:若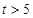 ,則銷售收入為
,則銷售收入為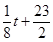 萬元.
萬元.
(1)若該公司的這種產品的年產量為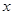 百件
百件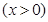 ,請把該公司生產并銷售這種產品所得的年利潤
,請把該公司生產并銷售這種產品所得的年利潤 表示為當年生產量
表示為當年生產量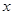 的函數;
的函數;
(2)當年產量為多少時,當年公司所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題12分)
某市居民生活用水收費標準如下:
用水量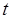 (噸) (噸) | 每噸收費標準(元) |
不超過 噸部分 噸部分 | 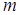 |
超過 噸不超過 噸不超過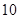 噸部分 噸部分 | 3 |
超過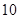 噸部分 噸部分 | 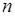 |
 噸,繳納的水費為
噸,繳納的水費為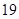 元;二月份用水量為
元;二月份用水量為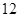 噸,繳納的水費為
噸,繳納的水費為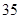 元.設某用戶月用水量為
元.設某用戶月用水量為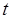 噸,交納的水費為
噸,交納的水費為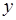 元.
元.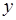 關于
關于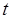 的函數關系式;
的函數關系式;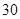 元,求該用戶三月份最多可以用多少噸水?
元,求該用戶三月份最多可以用多少噸水?查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com