
(1)求證:a⊥b;
(2)若存在不同時為零的實數(shù)k和t,使向量x=a+(t2-3)b,y=-ka+tb,且x⊥y,試求函數(shù)關(guān)系式k=f(t);
(3)根據(jù)(2)的結(jié)論,討論關(guān)于t的方程f(t)-k=0的解的情況.
(1)證明:∵a·b=(![]() ,-1)·(
,-1)·(![]() ,
,![]() )=
)=![]() ×
×![]() +(-1)×
+(-1)×![]() =
=![]() -
-![]() =0,∴a⊥b.
=0,∴a⊥b.
(2)解法一:∵x⊥y,∴x·y=0,
即[a+(t2-3)·b]·(-ka+tb)=0,
整理后得-ka2+[t-k(t2-3)]a·b+t(t2-3)·b2=0.
∵a·b=0,a2=(![]() )2+(-1)2=4,b2=(
)2+(-1)2=4,b2=(![]() )2+(
)2+(![]() )2=1,
)2=1,
∴上式化為-4k+t(t2-3)=0.
∴k=![]() t(t2-3).
t(t2-3).
解法二:x=a+(t2-3)b=(![]() ,-1)+(t2-3)·(
,-1)+(t2-3)·(![]() ,
,![]() )
)
=(![]() +
+![]() )
)
=(![]() ),y=-ka+tb
),y=-ka+tb
=-k(![]() ,-1)+t(
,-1)+t(![]() ,
,![]() )
)
=(-![]() k+
k+![]() ,k+
,k+![]() t)
t)
=(![]() ).
).
∵x⊥y,∴x·y=0.
∴![]() =
=![]() (t2+2
(t2+2![]() -3)·(t-2
-3)·(t-2![]() k)+
k)+![]() (
(![]() t2-2-3
t2-2-3![]() )·(2k+
)·(2k+![]() t)=0.
t)=0.
∴t(t2+2![]() -3)-2
-3)-2![]() k·(t2+2
k·(t2+2![]() -3)+2k(
-3)+2k(![]() t2-2-3
t2-2-3![]() )+
)+![]() t(
t(![]() t2-2-3
t2-2-3![]() )=0.
)=0.
∴k(2![]() t2-4-6
t2-4-6![]() -2
-2![]() t2-12+6
t2-12+6![]() )+t3+2
)+t3+2![]() t-3t+3t3-2
t-3t+3t3-2![]() t-9t=0.
t-9t=0.
∴-16k=-4t3+12t.
∴k=![]() t(t2-3).
t(t2-3).
∴k=f(t)=![]() t(t2-3).
t(t2-3).
(3)解:討論方程![]() t(t2-3)-k=0的解的情況,其實就是利用曲線f(t)=
t(t2-3)-k=0的解的情況,其實就是利用曲線f(t)= ![]() t(t2-3)的形狀及有關(guān)性質(zhì)(極值問題,單調(diào)性問題等)與曲線y=k(常量函數(shù))的交點個數(shù)問題.
t(t2-3)的形狀及有關(guān)性質(zhì)(極值問題,單調(diào)性問題等)與曲線y=k(常量函數(shù))的交點個數(shù)問題.
利用導數(shù)知識可以求出f′(t)=![]() ·(3t2-3)=
·(3t2-3)=![]() (t2-1)=
(t2-1)=![]() (t+1)(t-1).
(t+1)(t-1).
令f′(t)=0,解得t1=-1,t2=1.當t變化時,f′(t)、f(t)的變化情況如下表:
T | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
f′(t) | + | 0 | - | 0 | + |
f(t) | ? | 極大值 |
| 極小值 |
|
當t=-1時,f(t)有極大值,f(t)極大值=![]() ;
;
當t=1時,f(t)有極小值,f(t)極小值=-![]() .
.
而f(t)=![]() t(t2-3)=0時,得t(t2-3)=0,
t(t2-3)=0時,得t(t2-3)=0,
∴t=0,t=±![]() .
.
而t=±1是函數(shù)f(t)的兩個拐點,f(t)是奇函數(shù),所以f(t)的圖象大致如下圖所示:
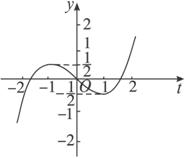
于是當k>![]() 或k<-
或k<-![]() 時,直線y=k與曲線y=f(t)僅有一個交點,則方程有一解;
時,直線y=k與曲線y=f(t)僅有一個交點,則方程有一解;
當k=![]() 或k=-
或k=-![]() 時,直線與曲線有兩個交點,則方程有兩個解;
時,直線與曲線有兩個交點,則方程有兩個解;
當k=0時,直線y=k與曲線y=f(t)有三個交點,但已知條件k與t不能同時為0,所以此時也只有兩解;
當-![]() <k<0或0<k<
<k<0或0<k<![]() 時,直線y=k與曲線y=f(t)有三個交點,則方程有三個解.
時,直線y=k與曲線y=f(t)有三個交點,則方程有三個解.
綜上所述,當k>![]() 或k<-
或k<-![]() 時,方程f(t)-k=0有一解;當k=±
時,方程f(t)-k=0有一解;當k=±![]() 時,方程f(t)-k=0有兩解;當k=0時,方程f(t)-k=0有兩解;當-
時,方程f(t)-k=0有兩解;當k=0時,方程f(t)-k=0有兩解;當-![]() <k<0或0<k<
<k<0或0<k<![]() 時,方程f(t)-k=0有三解.
時,方程f(t)-k=0有三解.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學 來源: 題型:
| a |
| 3 |
| b |
| 1 |
| 2 |
| ||
| 2 |
| x |
| a |
| b |
| y |
| a |
| b |
| x |
| y |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com