
【題目】給定橢圓![]() .稱圓心在原點O,半徑為
.稱圓心在原點O,半徑為![]() 的圓是橢圓C的“準(zhǔn)圓”.若橢圓C的一個焦點為
的圓是橢圓C的“準(zhǔn)圓”.若橢圓C的一個焦點為![]() ,其短軸上的一個端點到F的距離為
,其短軸上的一個端點到F的距離為![]() .
.
(1)求橢圓C的方程和其“準(zhǔn)圓”方程;
(2)點P是橢圓C的“準(zhǔn)圓”上的一個動點,過動點P作直線![]() ,使得
,使得![]() 與橢圓C都只有一個交點,試判斷
與橢圓C都只有一個交點,試判斷![]() 是否垂直?并說明理由.
是否垂直?并說明理由.
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)垂直.
;(Ⅱ)垂直.
【解析】
試題(1)由“橢圓C的一個焦點為![]() ,其短軸上的一個端點到F的距離為
,其短軸上的一個端點到F的距離為![]() ”知:
”知:![]() 從而可得橢圓的標(biāo)準(zhǔn)方程和“準(zhǔn)圓”的方程;
從而可得橢圓的標(biāo)準(zhǔn)方程和“準(zhǔn)圓”的方程;
(2)分兩種情況討論:①![]() 當(dāng)中有一條直線斜率不存在;②直線
當(dāng)中有一條直線斜率不存在;②直線![]() 斜率都存在.
斜率都存在.
對于①可直接求出直線![]() 的方程并判斷其是不互相垂直;
的方程并判斷其是不互相垂直;
對于②設(shè)經(jīng)過準(zhǔn)圓上點![]() 與橢圓只有一個公共點的直線為
與橢圓只有一個公共點的直線為![]()
與橢圓方程聯(lián)立組成方程組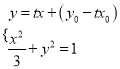 消去
消去![]() 得到關(guān)于
得到關(guān)于![]() 的方程:
的方程:![]()
由![]() 化簡整理得:
化簡整理得:![]()
![]()
![]()
而直線![]() 的斜率正是方程的兩個根
的斜率正是方程的兩個根![]() ,從而
,從而![]()
![]()
(1)![]()
![]() 橢圓方程為
橢圓方程為![]()
準(zhǔn)圓方程為![]()
(2)①![]() 當(dāng)中有一條無斜率時,不妨設(shè)
當(dāng)中有一條無斜率時,不妨設(shè)![]() 無斜率,
無斜率,
因為![]() 與橢圓只有一個共公點,則其方程為
與橢圓只有一個共公點,則其方程為![]()
當(dāng)![]() 方程為
方程為![]() 時,此時
時,此時![]() 與準(zhǔn)圓交于點
與準(zhǔn)圓交于點![]()
此時經(jīng)過點![]() (或
(或![]() )且與橢圓只有一個公共瞇的直線是
)且與橢圓只有一個公共瞇的直線是![]() (或
(或![]() )
)
即![]() 為
為![]() (或
(或![]() ),顯然直線
),顯然直線![]() 垂直;
垂直;
同理可證![]() 方程為
方程為![]() 時,直線
時,直線![]() 也垂直.
也垂直.
②當(dāng)![]() 都有斜率時,設(shè)點
都有斜率時,設(shè)點![]() 其中
其中![]()
設(shè)經(jīng)過點![]() 與橢圓只有一個公共點的直線為
與橢圓只有一個公共點的直線為![]()
則由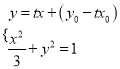 消去
消去![]() ,得
,得
![]()
由![]() 化簡整理得:
化簡整理得:![]()
因為![]() ,所以有
,所以有![]()
設(shè)![]() 的斜率分別為
的斜率分別為![]() ,因為
,因為![]() 與橢圓只有一個公共點
與橢圓只有一個公共點
所以![]() 滿足上述方程
滿足上述方程![]()
所以![]() ,即
,即![]() 垂直,
垂直,
綜合①②知,![]() 垂直.
垂直.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】某種水果按照果徑大小可分為四類:標(biāo)準(zhǔn)果、優(yōu)質(zhì)果、精品果、禮品果.某采購商從采購的一批水果中隨機抽取![]() 個,利用水果的等級分類標(biāo)準(zhǔn)得到的數(shù)據(jù)如下:
個,利用水果的等級分類標(biāo)準(zhǔn)得到的數(shù)據(jù)如下:
等級 | 標(biāo)準(zhǔn)果 | 優(yōu)質(zhì)果 | 精品果 | 禮品果 |
個數(shù) | 10 | 30 | 40 | 20 |
(1)若將頻率是為概率,從這![]() 個水果中有放回地隨機抽取
個水果中有放回地隨機抽取![]() 個,求恰好有
個,求恰好有![]() 個水果是禮品果的概率.(結(jié)果用分?jǐn)?shù)表示)
個水果是禮品果的概率.(結(jié)果用分?jǐn)?shù)表示)
(2)用樣本估計總體,果園老板提出兩種購銷方案給采購商參考.
方案![]() :不分類賣出,單價為
:不分類賣出,單價為![]() 元
元![]() .
.
方案![]() :分類賣出,分類后的水果售價如下:
:分類賣出,分類后的水果售價如下:
等級 | 標(biāo)準(zhǔn)果 | 優(yōu)質(zhì)果 | 精品果 | 禮品果 |
售價(元/kg) | 16 | 18 | 22 | 24 |
從采購單的角度考慮,應(yīng)該采用哪種方案?
(3)用分層抽樣的方法從這![]() 個水果中抽取
個水果中抽取![]() 個,再從抽取的
個,再從抽取的![]() 個水果中隨機抽取
個水果中隨機抽取![]() 個,
個,![]() 表示抽取的是精品果的數(shù)量,求
表示抽取的是精品果的數(shù)量,求![]() 的分布列及數(shù)學(xué)期望
的分布列及數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓C經(jīng)過A(5,3),B(4,4)兩點,且圓心在x軸上.
(1)求圓C的標(biāo)準(zhǔn)方程;
(2)若直線l過點(5,2),且被圓C所截得的弦長為6,求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)在線段![]() 上,是否存在一點
上,是否存在一點![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ?如果存在,求
?如果存在,求![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市疾控中心流感監(jiān)測結(jié)果顯示,自![]() 年
年![]() 月起,該市流感活動一度出現(xiàn)上升趨勢,尤其是
月起,該市流感活動一度出現(xiàn)上升趨勢,尤其是![]() 月以來,呈現(xiàn)快速增長態(tài)勢,截止目前流感病毒活動度仍處于較高水平,為了預(yù)防感冒快速擴散,某校醫(yī)務(wù)室采取積極方式,對感染者進行短暫隔離直到康復(fù).假設(shè)某班級已知
月以來,呈現(xiàn)快速增長態(tài)勢,截止目前流感病毒活動度仍處于較高水平,為了預(yù)防感冒快速擴散,某校醫(yī)務(wù)室采取積極方式,對感染者進行短暫隔離直到康復(fù).假設(shè)某班級已知![]() 位同學(xué)中有
位同學(xué)中有![]() 位同學(xué)被感染,需要通過化驗血液來確定感染的同學(xué),血液化驗結(jié)果呈陽性即為感染,呈陰性即未被感染.下面是兩種化驗方法: 方案甲:逐個化驗,直到能確定感染同學(xué)為止;
位同學(xué)被感染,需要通過化驗血液來確定感染的同學(xué),血液化驗結(jié)果呈陽性即為感染,呈陰性即未被感染.下面是兩種化驗方法: 方案甲:逐個化驗,直到能確定感染同學(xué)為止;
方案乙:先任取![]() 個同學(xué),將它們的血液混在一起化驗,若結(jié)果呈陽性則表明感染同學(xué)為這
個同學(xué),將它們的血液混在一起化驗,若結(jié)果呈陽性則表明感染同學(xué)為這![]() 位中的
位中的![]() 位,后再逐個化驗,直到能確定感染同學(xué)為止;若結(jié)果呈陰性則在另外
位,后再逐個化驗,直到能確定感染同學(xué)為止;若結(jié)果呈陰性則在另外![]() 位同學(xué)中逐個檢測;
位同學(xué)中逐個檢測;
(1)求依方案甲所需化驗次數(shù)等于方案乙所需化驗次數(shù)的概率;
(2)![]() 表示依方案甲所需化驗次數(shù),
表示依方案甲所需化驗次數(shù),![]() 表示依方案乙所需化驗次數(shù),假設(shè)每次化驗的費用都相同,請從經(jīng)濟角度考慮那種化驗方案最佳.
表示依方案乙所需化驗次數(shù),假設(shè)每次化驗的費用都相同,請從經(jīng)濟角度考慮那種化驗方案最佳.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 滿足:
滿足:![]() ,
,![]() ,其中
,其中![]() ,數(shù)列
,數(shù)列![]() 滿足:
滿足:![]()
(1)當(dāng)![]() 時,求
時,求![]() 的值;
的值;
(2)證明:![]() 對任意
對任意![]() 均成立,并求數(shù)列
均成立,并求數(shù)列![]() 的通項公式;
的通項公式;
(3)是否存在正數(shù)![]() ,使得數(shù)列
,使得數(shù)列![]() 的每一項均為整數(shù),如果不存在,說明理由,如果存在,求出所有的
的每一項均為整數(shù),如果不存在,說明理由,如果存在,求出所有的![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,求
時,求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當(dāng)![]() 時,關(guān)于
時,關(guān)于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給定直線m:y=2x-16,拋物線C:y2=ax(a>0).
(1)當(dāng)拋物線C的焦點在直線m上時,確定拋物線C的方程;
(2)若△ABC的三個頂點都在(1)所確定的拋物線C上,且點A的縱坐標(biāo)y=8,△ABC的重心恰在拋物線C的焦點上,求直線BC的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在四棱錐P-ABCD中,底面ABCD是梯形,AB∥DC,AD⊥DC,AB=AD=2,DC=3,平面PDC⊥平面ABCD,E在棱PC上且PE=2EC。
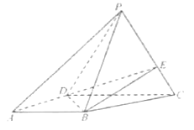
()證明:BE∥平面PAD;
(1)若ΔPDC是正三角形,求三棱錐P-DBE的體積。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com