
【題目】如圖,菱形ABCD和直角梯形CDEF所在平面互相垂直,![]()
![]() .
.
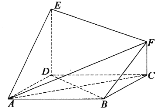
(1)求證:![]() ;
;
(2)求四棱錐![]() 的體積.
的體積.
【答案】(1)見解析;(2)![]()
【解析】
(1)本題首先可以通過菱形![]() 和直角梯形
和直角梯形![]() 所在平面互相垂直來證明出
所在平面互相垂直來證明出![]() 平面
平面![]() ,然后通過
,然后通過![]() 平面
平面![]() 證明出
證明出![]() ,再通過菱形的性質(zhì)證明出
,再通過菱形的性質(zhì)證明出![]() ,最后通過線面垂直的相關(guān)性質(zhì)即可證明出
,最后通過線面垂直的相關(guān)性質(zhì)即可證明出![]() 平面
平面![]() 以及
以及![]() ;
;
(2)本題首先可以過點![]() 向
向![]() 做垂線,垂線就是四棱錐
做垂線,垂線就是四棱錐![]() 的高,再通過四棱錐
的高,再通過四棱錐![]() 的體積公式即可得出結(jié)果。
的體積公式即可得出結(jié)果。
(1)因為![]() ,
,![]() ,所以
,所以![]() ,
,
又因為平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因為![]() 平面
平面![]() ,所以
,所以![]() ,
,
因為四邊形![]() 是菱形,所以
是菱形,所以![]() ,
,
又因為![]() 平面
平面![]() 、
、![]() 平面
平面![]() 、
、![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因為![]() 平面
平面![]() ,所以
,所以![]() ;
;
(2)
如圖所示,過點![]() 向
向![]() 做垂線,垂足為
做垂線,垂足為![]() ,即
,即![]() ,
,
因為平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
在直角三角形![]() 中有
中有![]() 、
、![]() ,所以
,所以![]() ,
,
所以四棱錐![]() 的體積
的體積![]() 。
。


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知點F是拋物線C:y2=2px(p>0)的焦點,點M(x0,1)在C上,且|MF|=![]() .
.
(1)求p的值;
(2)若直線l經(jīng)過點Q(3,-1)且與C交于A,B(異于M)兩點,證明:直線AM與直線BM的斜率之積為常數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系xOy中,以原點O為極點,x軸的正半軸為極軸建立極坐標系,已知直線l的參數(shù)方程為: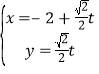 ,
,![]() 為參數(shù)
為參數(shù)![]() 點的極坐標為
點的極坐標為![]() ,曲線C的極坐標方程為
,曲線C的極坐標方程為![]() .
.
![]() Ⅰ
Ⅰ![]() 試將曲線C的極坐標方程化為直角坐標方程,并求曲線C的焦點在直角坐標系下的坐標;
試將曲線C的極坐標方程化為直角坐標方程,并求曲線C的焦點在直角坐標系下的坐標;
![]() Ⅱ
Ⅱ![]() 設(shè)直線l與曲線C相交于兩點A,B,點M為AB的中點,求
設(shè)直線l與曲線C相交于兩點A,B,點M為AB的中點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某工廠為提高生產(chǎn)效率,開展技術(shù)創(chuàng)新活動,提出了完成某項生產(chǎn)任務的兩種新的生產(chǎn)方式.為比較兩種生產(chǎn)方式的效率,選取40名工人,將他們隨機分成兩組,每組20人,第一組工人用第一種生產(chǎn)方式,第二組工人用第二種生產(chǎn)方式.根據(jù)工人完成生產(chǎn)任務的工作時間(單位:min)繪制了莖葉圖:則下列結(jié)論中表述不正確的是
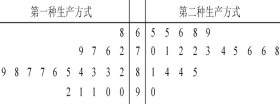
A. 第一種生產(chǎn)方式的工人中,有75%的工人完成生產(chǎn)任務所需要的時間至少80分鐘
B. 第二種生產(chǎn)方式比第一種生產(chǎn)方式的效率更高
C. 這40名工人完成任務所需時間的中位數(shù)為80
D. 無論哪種生產(chǎn)方式的工人完成生產(chǎn)任務平均所需要的時間都是80分鐘.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,橢圓C過點
中,橢圓C過點![]() ,焦點
,焦點![]() ,圓O的直徑為
,圓O的直徑為![]() .
.

(1)求橢圓C及圓O的方程;
(2)設(shè)直線l與圓O相切于第一象限內(nèi)的點P.
①若直線l與橢圓C有且只有一個公共點,求點P的坐標;
②直線l與橢圓C交于![]() 兩點.若
兩點.若![]() 的面積為
的面積為![]() ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知平面直角坐標系![]() 中,過點
中,過點![]() 的直線l的參數(shù)方程為
的直線l的參數(shù)方程為![]() (t為參數(shù)),以原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為
(t為參數(shù)),以原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為![]() 與曲線C相交于不同的兩點M,N.
與曲線C相交于不同的兩點M,N.
(1)求曲線C的直角坐標方程和直線l的普通方程;
(2)若![]() ,求實數(shù)a的值.
,求實數(shù)a的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】邗江中學高二年級某班某小組共10人,利用寒假參加義工活動,已知參加義工活動次數(shù)為1,2,3的人數(shù)分別為3,3,4.現(xiàn)從這10人中選出2人作為該組代表參加座談會.
(1)記“選出2人參加義工活動的次數(shù)之和為4”為事件![]() ,求事件
,求事件![]() 發(fā)生的概率;
發(fā)生的概率;
(2)設(shè)![]() 為選出2人參加義工活動次數(shù)之差的絕對值,求隨機變量
為選出2人參加義工活動次數(shù)之差的絕對值,求隨機變量![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com