【題目】已知曲線C：x2+y2-2x-4y+m=0
（1）當m為何值時，曲線C表示圓；
（2）若曲線C與直線x+2y-4=0交于M、N兩點，且OM⊥ON(O為坐標原點)，求m的值。
【答案】（1）m<5；（2）m=
.
【解析】試題分析：（1）由二元二次方程表示圓的條件D2+E2-4F大于0列出關于m的不等式，求出不等式的解集即可得到m的取值范圍；（2）設出曲線與直線的交點M和N的坐標，聯立曲線C與直線的方程，消去y后得到關于x的一元二次方程，利用韋達定理表示出兩根之和與兩根之積，然后由OM與ON垂直得到M和N橫坐標之積與縱坐標之積的和為0，由直線方程化為橫坐標的關系式，把表示出的兩根之和與兩根之積代入即可求出m的值．
試題解析：
（1）由D2+E2-4F=4+16-4m=20-4m>0，得m<5
（2）設M(x1,y1),N(x2,y2)，由OM⊥ON得x1x2+ y1y2=0.
將直線方程x+2y-4=0與曲線C：x2+y2-2x-4y+m=0聯立并消去y得
5x2-8x+4m-16=0，由韋達定理得x1+x2=
①,x1x2=
②，
=64-20（4m-16）=384-80m﹥0﹥所以m﹤4
又由x+2y-4=0得y=
(4-x),
∴x1x2+y1y2=x1x2+
(4-x1)·
(4-x2)= 
x1x2-( x1+x2)+4=0.
將①、②代入得m=
,滿足
﹥ 0.
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=|x﹣1|﹣|x+1|．
（1）求不等式|f（x）|＜1的解集；
（2）若不等式|a|f（x）≥|f（a）|對任意a∈R恒成立，求實數x的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設z1 ， z2是復數，給出下列四個命題： ①若|z1﹣z2|=0，則 
= 
②若z1= ，則 =z2
③若|z1|=|z2|，則z1 =z2 ④若|z1|=|z2|，則z12=z22
其中真命題的序號是 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
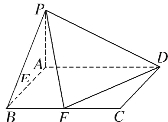
【題目】已知在四棱錐
中，底面
是矩形，且
，
，
平面
，
、
分別是線段
、
的中點．
（1）證明：
（2）在線段
上是否存在點
，使得
∥平面
，若存在，確定點的位置；若不存在，說明理由．
（3）若
與平面
所成的角為
，求二面角
的余弦值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（
，
）的一系列對應值如表：
（1）根據表格提供的數據求函數
的一個解析式；
（2）根據（1）的結果：
①當
時，方程
恰有兩個不同的解，求實數
的取值范圍；
②若
，
是銳角三角形的兩個內角，試比較
與
的大小．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
