Question

【題目】已知點在拋物線：上．

（1）求的方程；

（2）過上的任一點（與的頂點不重合）作軸于，試求線段中點的軌跡方程；

（3）在上任取不同于點的點，直線與直線交于點，過點作軸的垂線交拋物線于點，求面積的最小值．

Answer 1

【答案】（1）（2）（3）面積的最小值為．

【解析】

（1）將點的坐標代入拋物線方程即可求解；

（2）設中點的坐標，并用坐標坐標表示點的坐標，代入拋物線方程即可，另外排除； （3）方法一，設點A的坐標，寫出直線的方程，并與直線方程聯立，求解點P的坐標，進而寫點B坐標，判斷直線AB過定點，根據與點，將分割成與，用與的面積和表示所求，進而求最值；方法二，設點A的坐標，由向量共線求點P坐標，進而求點B坐標，是上的一點，由向量共線證明直線AB過定點，根據與點，將分割成與，進而用點A、B的縱坐標表示面積，可求最值；方法三，設直線：，與拋物線方程聯立，由韋達定理得點A、B的縱坐標的關系。用點B坐標表示點P的坐標，由A、C、P三點共線推出m,n的關系，進而可得直線過定點，根據與點，將分割成與，進而用點A、B的縱坐標表示面積，可求最值。

解：（1）依題意，得，

所以，

從而的方程為．

（2）設線段中點的坐標為，則點的坐標為．

由點在上，得

化簡得，顯然，

所以線段中點的軌跡方程為．

（3）方法一：設點的坐標為，

則直線的方程為，

由解得，

即點的坐標為，

因為軸，過點在拋物線上，

所以的點坐標為．

故當時，點坐標為，點坐標為，直線過定點；…

當時，顯然，

故直線的方程可為，

化簡得．

因為任意，故，解得，

所以，直線也過定點．

于是，可設直線的方程為，且，，

由得，

則，，

，

所以當時，的面積最小值為．此時，易得、兩點的坐標可分別為

、．

方法二：因是拋物線上不同于點的點，故可設點，

又點在直線上，故可設點，

由、、三點共線得，而，，

所以點的縱坐標為，

因此，點的坐標為．

因為軸，且點在拋物線上，所以點坐標為，

設是上的一點，則，

而，，

所以，

即，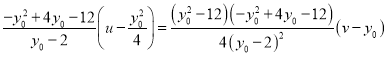

又．

所以，

即．

整理得

因任意，故，解得，

故直線過定點．

由此可得，不妨設點在點的上方，則．

于是的面積為

．

顯然，當時等號成立，故面積的最小值為，此時，易得、兩點的坐標可分為、．

方法三，設直線：，則由得，

設，，則，

因為軸，所以點的縱坐標為，

又點在直線上，所以點的坐標為，

因為、、三個共線，所以，而，，

所以．

又，所以，

即．…………（*）

將、代入（*）．

得．

即．因為任意，所以．…

即，故直線過定點．

由此可得，于是的面積為

，

所以當時，的面積的最小值為．此時，易得、兩點的坐標可分別為、．