
【題目】已知函數![]() =lnx+ax2+(2a+1)x.
=lnx+ax2+(2a+1)x.
(1)討論![]() 的單調性;
的單調性;
(2)當a﹤0時,證明![]() .
.
【答案】(1)見解析;(2)見解析.
【解析】試題分析:(1)先求函數導數![]() ,再根據導函數符號的變化情況討論單調性:當
,再根據導函數符號的變化情況討論單調性:當![]() 時,
時, ![]() ,則
,則![]() 在
在![]() 單調遞增;當
單調遞增;當![]() 時,
時, ![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減.(2)證明
單調遞減.(2)證明![]() ,即證
,即證![]() ,而
,而![]() ,所以需證
,所以需證![]() ,設g(x)=lnx-x+1 ,利用導數易得
,設g(x)=lnx-x+1 ,利用導數易得![]() ,即得證.
,即得證.
試題解析:(1)f(x)的定義域為(0,+![]() ),
),![]() .
.
若a≥0,則當x∈(0,+![]() )時,
)時, ![]() ,故f(x)在(0,+
,故f(x)在(0,+![]() )單調遞增.
)單調遞增.
若a<0,則當x∈![]() 時,
時, ![]() ;當x∈
;當x∈![]() 時,
時, ![]() .故f(x)在
.故f(x)在![]() 單調遞增,在
單調遞增,在![]() 單調遞減.
單調遞減.
(2)由(1)知,當a<0時,f(x)在![]() 取得最大值,最大值為
取得最大值,最大值為
![]() .
.
所以![]() 等價于
等價于![]() ,即
,即![]() .
.
設g(x)=lnx-x+1,則![]() .
.
當x∈(0,1)時, ![]() ;當x∈(1,+
;當x∈(1,+![]() )時,
)時, ![]() .所以g(x)在(0,1)單調遞增,在(1,+
.所以g(x)在(0,1)單調遞增,在(1,+![]() )單調遞減.故當x=1時,g(x)取得最大值,最大值為g(1)=0.所以當x>0時,g(x)≤0.從而當a<0時,
)單調遞減.故當x=1時,g(x)取得最大值,最大值為g(1)=0.所以當x>0時,g(x)≤0.從而當a<0時, ![]() ,即
,即![]() .
.


 走進文言文系列答案
走進文言文系列答案科目:高中數學 來源: 題型:
【題目】【2017安徽淮北二模】選修4—4:坐標系與參數方程
在直角坐標系![]() 中, 以
中, 以![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標系, 圓
軸正半軸為極軸建立極坐標系, 圓![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為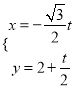 (t為參數), 直線
(t為參數), 直線![]() 和圓
和圓![]() 交于
交于![]() 兩點。
兩點。
(Ⅰ)求圓心的極坐標;
(Ⅱ)直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]在平面坐標系中xOy中,已知直線l的參考方程為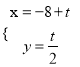 (t為參數),曲線C的參數方程為
(t為參數),曲線C的參數方程為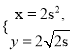 (s為參數)。設p為曲線C上的動點,求點P到直線l的距離的最小值
(s為參數)。設p為曲線C上的動點,求點P到直線l的距離的最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一元二次不等式ax2+bx+c>0的解集是(﹣ ![]() ,2),則cx2+bx+a<0的解集是( )
,2),則cx2+bx+a<0的解集是( )
A.(﹣3, ![]() )
)
B.(﹣∞,﹣3)∪( ![]() ,+∞)
,+∞)
C.(﹣2, ![]() )
)
D.(﹣∞,﹣2)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三棱柱ABC﹣A1B1C1的側面AA1C1C為正方形,側面AA1B1B⊥側面BB1C1C,且AC=2,AB= ![]() ,∠A1AB=45°,E、F分別為AA1、CC1的中點.
,∠A1AB=45°,E、F分別為AA1、CC1的中點. 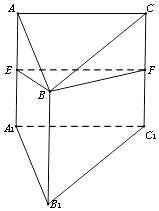
(1)求證:AA1⊥平面BEF;
(2)求二面角B﹣EB1﹣C1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:
(1)函數y=tanx在定義域內單調遞增;
(2)若α,β是銳角△ABC的內角,則sinα>cosβ;
(3)函數y=cos( ![]() x+
x+ ![]() )的對稱軸x=
)的對稱軸x= ![]() +kπ,k∈Z;
+kπ,k∈Z;
(4)函數y=sin2x的圖象向左平移 ![]() 個單位,得到y=sin(2x+
個單位,得到y=sin(2x+ ![]() )的圖象.
)的圖象.
其中正確的命題的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() :
: ![]() (
(![]() )的左右焦點分別為
)的左右焦點分別為![]() ,
, ![]() ,下頂點為
,下頂點為![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
(Ⅰ)求橢圓![]() 的離心率;
的離心率;
(Ⅱ)設![]() 為橢圓上異于其頂點的一點,
為橢圓上異于其頂點的一點, ![]() 到直線
到直線![]() 的距離為
的距離為![]() ,且三角形
,且三角形![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相切,過焦點
相切,過焦點![]() ,
, ![]() 分別作
分別作![]() ,
, ![]() ,垂足分別為
,垂足分別為![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】通過隨機詢問110名性別不同的行人,對過馬路是愿意走斑馬線還是愿意走人行天橋進行抽樣調查,得到如下的列聯表:
男 | 女 | 總計 | |
走天橋 | 40 | 20 | 60 |
走斑馬線 | 20 | 30 | 50 |
總計 | 60 | 50 | 110 |
由 ![]() ,算得
,算得 ![]()
參照獨立性檢驗附表,得到的正確結論是( )
A.有99%的把握認為“選擇過馬路的方式與性別有關”
B.有99%的把握認為“選擇過馬路的方式與性別無關”
C.在犯錯誤的概率不超過0.1%的前提下,認為“選擇過馬路的方式與性別有關”
D.在犯錯誤的概率不超過0.1%的前提下,認為“選擇過馬路的方式與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=cos(ωx+φ)(ω>0,﹣ ![]() <φ<0)的最小正周期為π,且f(
<φ<0)的最小正周期為π,且f( ![]() )=
)= ![]() .
. 
(1)求ω和φ的值;
(2)在給定坐標系中作出函數f(x)在[0,π]上的圖象.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com